Published: Apr 8, 2021 by Dev-hwon

A Deep Learning Model for Smart Manufacturing Using Convolutional LSTM Neural Network Autoencoders Aniekan Essien , Member, IEEE, and Cinzia Giannetti, 2020

A Deep Learning Model for Smart Manufacturing Using Convolutional LSTM Neural Network Autoencoders

ABSTRACT

• Machine Speed Prediction은 다양한 시스템 조건에 따라 생산 프로세스를 동적으로 조정하고 생산 처리량을 최적화하여 에너지 소비량을 최소화하는데 사용
• 정확한 데이터 기반 기계 속도 예측은 어렵다.
• 산업 제조 공정 데이터의 복잡한 특성을 감안할 때 noise에 강하고 입력 시계열 신호의 시간 및 공간 분포를 캡처 할 수 있는 예측 모델이 전제조건이 되어야 한다.
• End-to-End model for multistep machine speed prediction인 Deep convolutional LSTM encoder-decoder architechture를 제안

INTRODUCTION

• CNN은 주로 벡터 공간에서 작동하므로 입력 시계열의 고차원 features를 학습하는데는 어려움이 있다. 따라서 CNN은 시계열 예측 문제에서의 적용은 차선책이다.
• Convolutional LSTM(ConvLSTM)은 spatial information을 보존하고 sequential learning에 잘 수행한다.

• 2-DConvLSTMAE를 제안(Deep ConvLSTM stacked autoencoder for univariate, multistep machine speed forecasting)

  1) ConvLSTM encoding layers

  2) Bidirectional stacked LSTM decoding layers

  3) Time-distributed supervised learning[Fully connected(FC)] layers

• Input: 금속 캔 bodymaker 기계의 내부 속도 (분당 스트로크 수로 측정)

TECHNICAL PRELIMINARIES

A. Problem Formulation

• Multistep(sequence to sequence) 시계열 예측의 목표는 이전에 관찰된 입력 sequence를 이용하여 미래 시계열 값의 고정 길이 sequence를 예측하는 것
• Sequential 입력 데이터를 지도 학습 문제로 변환하는 sliding-window method를 사용
• 입력 시계열 sequence의 일부가 Input features로 사용되도록 재구성
• 이전 Time step을 window width/size로 나타낸다.
• 단변량 time series \(x(t)={x_1,x_2,\cdots,x_t}\)를 이용하여 미래의 k값들을 예측

\[\hat{y}=(\hat{y_1},\hat{y_2},\cdots,\hat{y_k})\cong(x_{t+1},x_{t+2},\cdots,x_{t+k})\]

• sliding window size로 나타내면 \(\hat{y}=(\hat{y_1},\hat{y_2},\cdots,\hat{y_k})=f(x_{t-w},x_{t-w+1},x_{t-w+2},\cdots,x_t)\)
• Input은 일정 기간(1분)동안 얻은 기계의 속도
• Input matrix : \(X\in\mathbb{R}^{n\times w}\), Output matrix : \(Y\in\mathbb{R}^{n\times k}\), Training samples의 갯수 : \(n=(N-w-k+1)\)

B. Structure of the CNN

• CNN은 주로 이미지, 비디오 인식에 사용되는 feedforward neural network

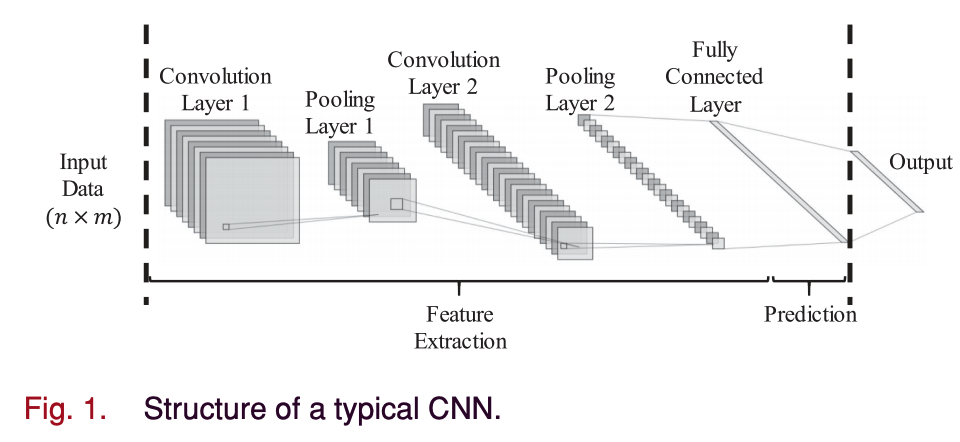
• Convolution 연산

\[\begin{aligned} y_{ij}=\sigma\begin{pmatrix}\sum^F_{r=1}\sum^F_{c=1}w_{rc}x_{(r+1\times S)(c+j\times S)}+b\end{pmatrix} \\ 0\leq 1\leq \frac{H-F}{S}, \;\;\;\; 0 \leq j \leq \frac{W-F}{S} \;\;\;\; \end{aligned}\]

• \(H\) : 높이, \(W\) : 너비, \(F\) : 커널의 크기, \(S\) : stride
• \(x_{(r+1\times S)(c+j\times S)}\)는 좌표 \((r+1 \times S)(c+j \times S)\)에 있는 입력 데이터 요소
• \(w_{rc}\) : 가중치, \(b\) : 편향, \(\sigma\) : 비선형 활성화 함수
• Input(size: \(H \times W \times D\))이 Convolution layer를 거치면 \((\frac{H-F+2P}{S+q})\times (\frac{W-F+2P}{S+1})\times k\) size로 바뀐다. (K는 필터의 개수)
• 이 process는 convolution layer stack이 깊어짐에 따라 점차적으로 차원을 감소

• pooling layer에는 두 가지 주요 기능이 있다.

  1. Input layer의 spatial dimension을 최대 75% 줄인다.
  2. 과적합을 제어한다.

C. LSTM Neural network

• Sequential data의 temporal dimension을 보존하는 RNN의 변형

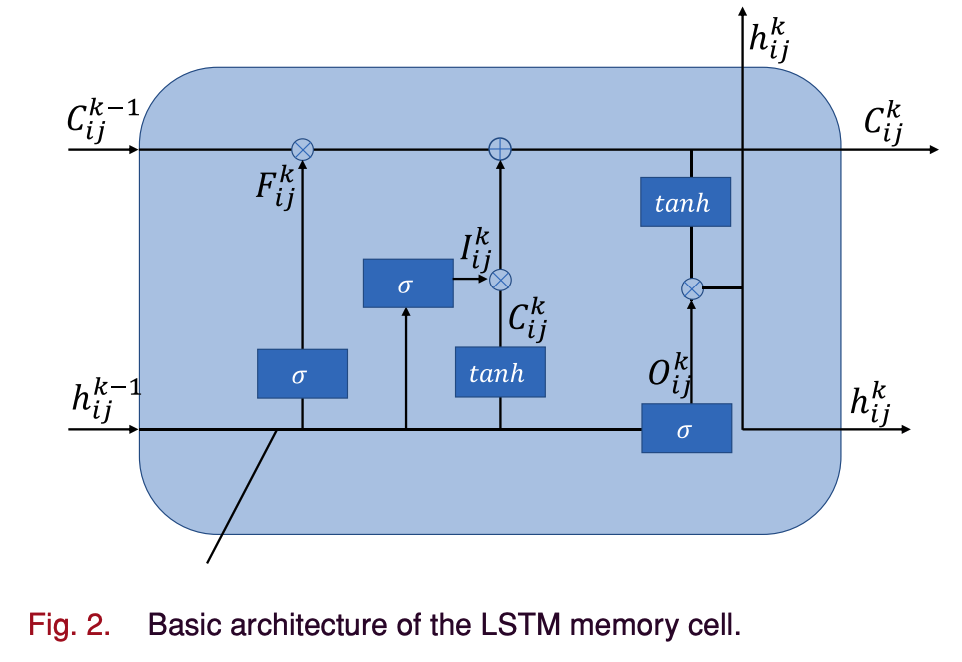
• LSTM memory cell은 크게 두 가지 구성요소를 가지고 있다.

  1) Long-term state component \(c_{(t)}\)

  2) Short-term state component \(h_{(t)}\)

• 세 개의 control gates(input, output, forget)를 통해 각 셀이 쓰기, 읽기, 리셋 기능을 한다.
• LSTM은 Multiplicative gates를 사용하여 RNN의 vanishing gradient 문제를 해결

\[\begin{aligned} i_{t}&=\sigma(W_{xi}x_t+W_{hi}h_{t-1}+W_{ci}C_{t-1}+b_i) \\ f_{t}&=\sigma(W_{xf}x_t+W_{hf}h_{t-1}+W_{cf}C_{t-1}+b_f) \\ c_{t}&=f_tC_{t-1}+i_tg(W_{xc}x_t+W_{hc}h_{t-1}+b_c) \\ o_{t}&=\sigma(W_{xo}x_t+W_{ho}h_{t-1}+W_{co}C_{t-1}+b_o) \\ h_{t}&=o_th(c_t) \end{aligned}\]

• \(W\) : 가중치 매트릭스, \(b\) : 편향 \(\sigma(.)\) : standard logistic sigmoid function
• \(i\) : input gate, \(f\) : forget gate, \(o\) : output gate

D. Convolutional LSTM

• ConvLSTM model은 FC layer 연산자를 Convolution 연산자로 대체하는 LSTM의 변형이다.
• 수식은 LSTM과 동일하나 Input vector \(x_t\)가 이미지이다.

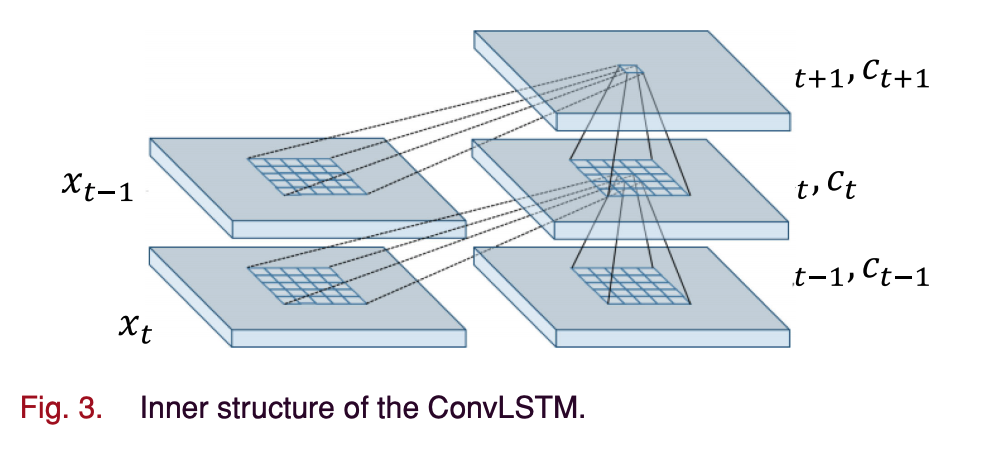
E. Autoencoder

• Input과 Output이 동일한 feedforward neural network
• Input으로 부터 features를 추출
• Three basic component : encoder, code, decoder
• encoder는 입력을 code로 압축하고 이후 decoder에 의해 디코딩 된다.
• autoencoder는 차원 축소 전략으로 사용 가능하다.

2-DConvLSTMAE MODEL

• 전체 model architechture

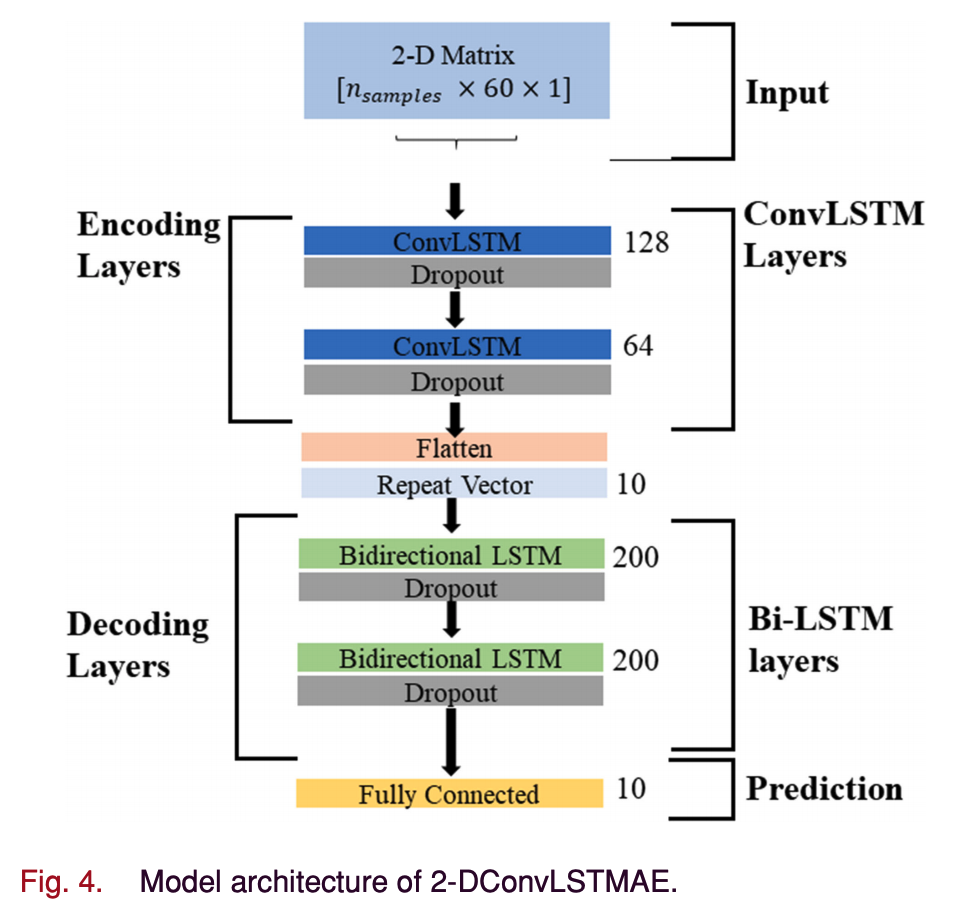
A. ConvLSTM Encoder

• ConvLSTM은 Sequence의 길이가 늘어나면 성능이 저하된다.
• 이를 해결하고자 attention-based mechanism을 적용한다.

\[\begin{aligned} i^{t,l}&=\sigma(W^l_{xz}x^{t,l}+W^l_{hz}h^{t-1,l}+W^l_{cz}\circ C^{t-1,l}+b^l_z) \\ f^{t,l}&=\sigma(W^l_{xr}x^{t,l}+W^l_{hr}h^{t-1,l}+W^l_{cr}\circ C^{t-1,l}+b^l_r) \\ c^{t,l}&=i^{t,l}\circ \mathrm{tanh}(W^l_{xc}x^{t,l}+W^l_{hc}h^{t,l}+b^l_c)+r^{t,l}\circ c^{t-1,l} \\ o^{t,l}&=\sigma(W^l_{xo}x^{t,l}+W^l_{ho}h^{t-1,l}+W^l_{co}C^{t,l}+b^l_o) \\ h_{t}&=o^{t,l}\circ\mathrm{tanh}(c^{t,l}) \end{aligned}\]

• \(\circ\) : Hadamard product, \(\sigma\) : sigmoid function
• \(W^l_{xz},W^l_{xr},W^l_{xc},W^l_{cr},W^l_{xc},W^l_{hc},W^l_{xo},W^l_{ho},W^l_{co}\in\mathbb{R}^{n\times T}\) : convolutional kernels
• \(b_z^l, b_r^l, b_c^l, b_o^l\) : lth layer의 bias parameters
• ConvLSTM Encoder architechture

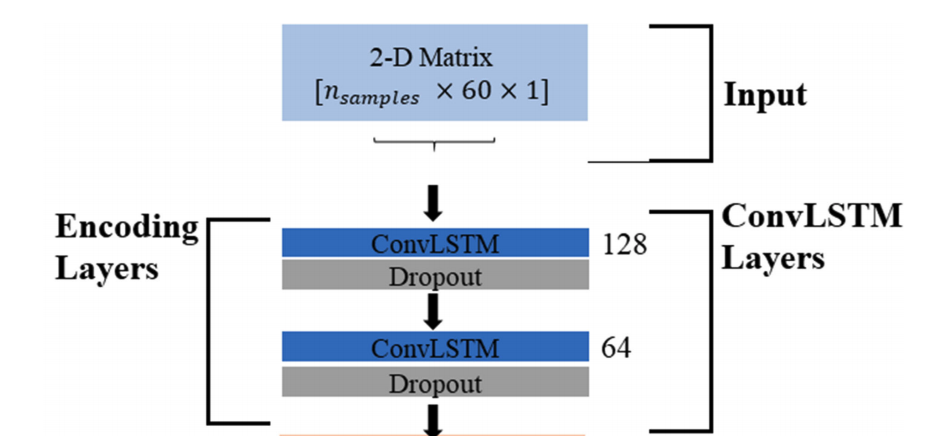
• ConvLSTM에서 Sequence의 길이는 모델 성능에 영향을 미치는 hyperparmeter이므로 최적화해야한다.
• Grid search framework를 이용하여 결정한다.

B. Bidirectional LSTM Decoder

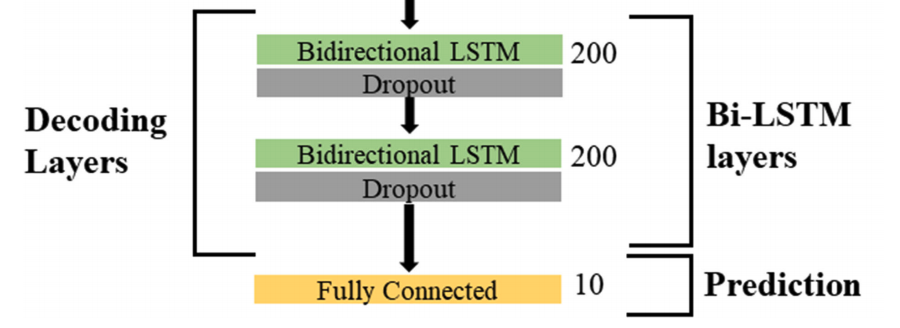
• encoder phase의 output은 \((n\times 1\times 8 \times 64)\)차원의 일련의 featrue map vactors (n은 학습 샘플의 수)
• 이 layer의 주요 기능은 decoder의 각 time step에 대한 일정한 input 형태로 encoding layer로 부터의 최종 output 벡터를 반복하는 것, 이러한 방식으로 decoding layer는 원래 입력 sequence를 재구성 한다.
• 이 반복 벡터 layer의 출력은 bidirectional LSTM stacked network로 전달한다.
• 각 LSTM은 ReLU가 적용된 200개의 LSTM 유닛으로 구성한다.
• 이전 LSTM layer의 출력은 계층적 방식으로 다음 layer에 입력으로 전달한다.
• 이런 방식으로 decoder layer는 ConvLSTM encoder의 encoding된 출력 벡터를 통합, 이는 개별 layer에서 representation larning을 강화하여 예측 모델의 성능을 향상시킨다.

C. hyperparmeter Optimization

• DL models의 성능은 optimization process를 사용하여 미리 결정된 hyperparmeters에 따라 달라진다.
• 이 제안 모델에서는 8개의 hyperparmeter가 최적화되었다.

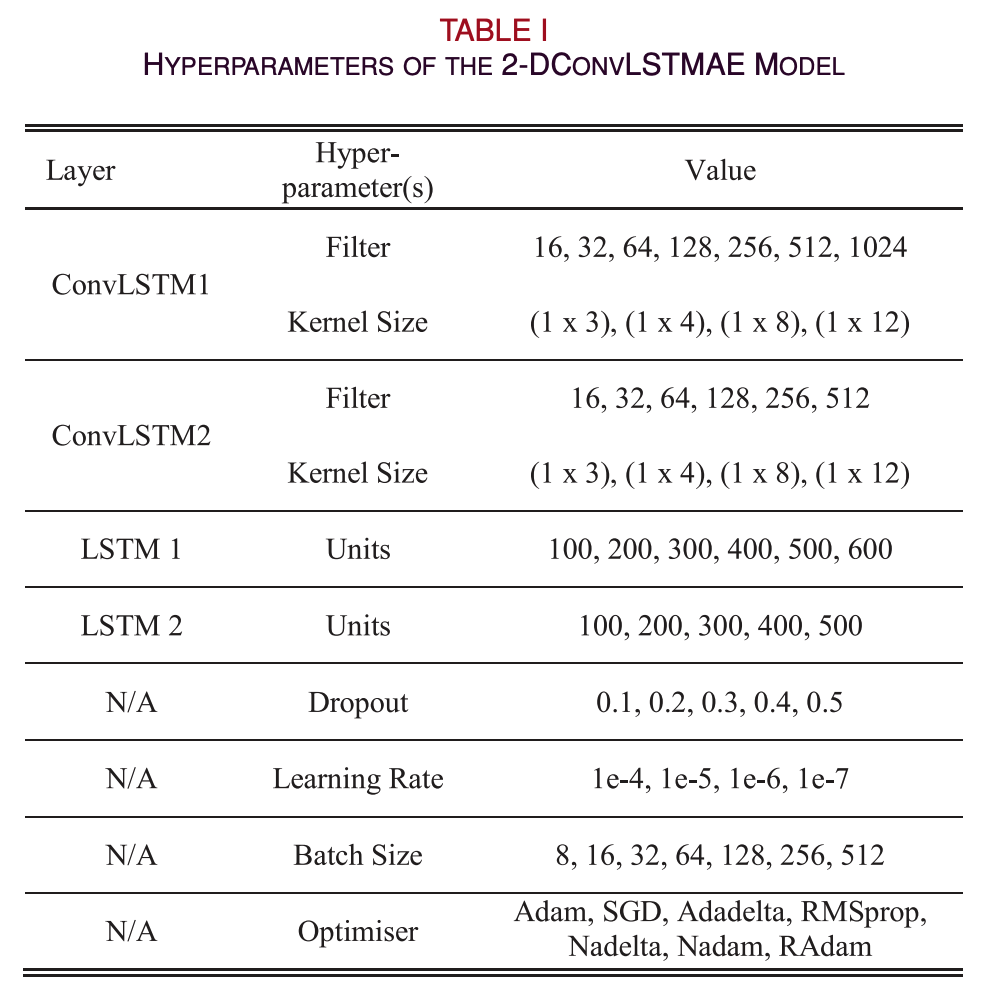
• hyperparmeter 최적화 방법으로는 random search, grid search, bayesian optimization 등이 있지만 grid search approch가 manual search와 비교하여 현재 연구과 같은 저차원 공간에서 신뢰성이 있기 때문에 제안하는 2-DConvLSTM와 baseline/competitor model 모두 grid framework를 적용하여 hyperparmeter를 최적화하였다.
• 또한 Grid search는 구현이 간단하며 병렬화를 쉽게 구성할 수 있다.

1. n개의 가능한 구성 hyperparmeter \(h\)의 인덱스를 갖는 집합 \(\forall\)이 주어지면, Grid search는 validation loss를 최소화하는 각 hyperparmeter \((h^1,\cdots,h^k)\)에 대한 values set을 선택

2. Grid search 시행 횟수가 \(S=\prod^n_{n=1}\begin{vmatrix}h^{(k)}\end{vmatrix}\)가 되도록 grid 형식의 모든 값을 조합한다.

D. Optimizer

• Optimization algorithm으로 Adam을 사용
• Learning late는 grid search framework에 의해 결정된 \(1\times 10^{-6}\)을 사용

E. Loss function

• RMSE 사용, 따라서 훈련 데이터에 대한 RMSE가 계산되고 역전파되어 각 epoch로 model parameter update.

\[\mathrm{RMSE}=\sqrt{\frac{1}{n}\sum^n_{i=1}(\hat{y}_i-y_i)^2}\]

• Adam optimizer를 사용하여 mini batch stocastic gradient descent 적용

EXPERIMENTS AND RESULTS

A. Data Preparation

• 사용된 데이터셋에는 \(\frac{1}{60}\)Hz의 주파수로 기계로부터 수집된 속도 데이터
• 데이터는 고속 알루미늄 캔 제조기계의 속도를 나타내며 분당 스트로크 수로 측정되고 기계에 내부적으로 기록
• bodymaker 기계는 일련의 철링을 통과하는 작은 금속 컵에서 전체 길이의 캔 body를 생산한다.
• 기계의 작동 속도는 생산 처리량과 수율에 영향을 끼친다.
• 일반적으로 정상적인 생산 일정과 연결된 주기적 패턴과 비정상적인 작업으로 인한 일시적이고 산발적인 패턴의 혼합으로 이루어져 있다.
• 또한 이 기계는 커퍼(선공정) 및 캔 세척/살균(후공정) 기계와 같은 선후 공정에 영향을 미치며 받는다.
• 데이터 셋은 2017년 8월 31일 00:00에서 2018년 8월 30일 23:59분 사이의 분 단위 기계 속도(스트로크/분)에 대한 525,600개의 관측값이다.
• 그 중 463,978개를 training set으로 51,533개를 test set, 10,000개를 validation set으로 사용한다.
• sequential supervised learning을 위한 적합한 형식으로 변환한다.
• sliding window size w=60으로, recurrent step size을 1로 하고 예측 간격 k=10분으로 하였다.

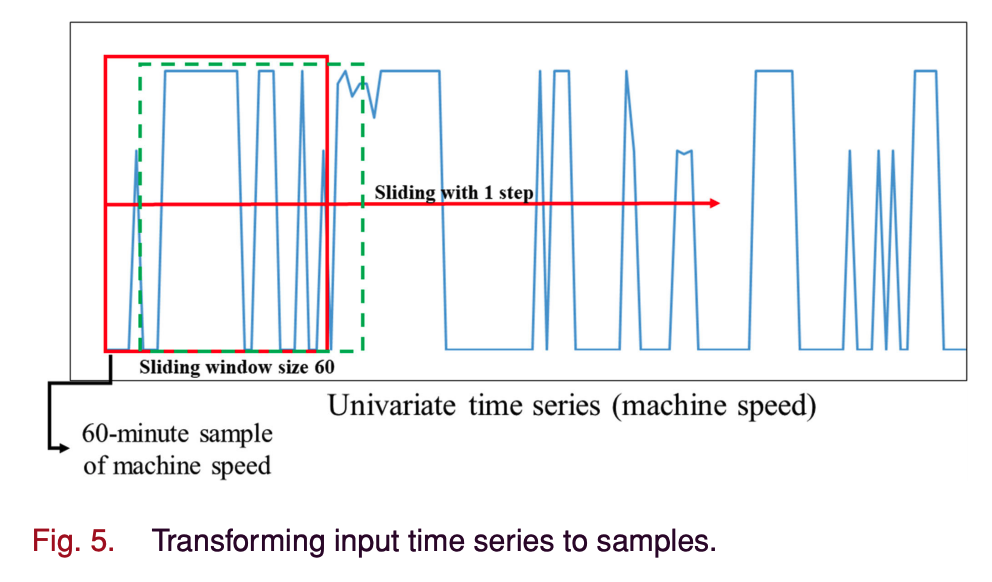
• Input size의 변화

\(x(t)=\{x_1,x_2,\cdots,x_N\} \text{ shape :} (N\times1)\) 에서 \((n\times 60 \times 1)\)로 바뀐다. \(n=(N-k-w+1)=525,531\)

B. Baseline Models

1. Persistence Model

• 대상 변수의 예측값이 이전 time lag와 동일하게 유지 된다는 가정.
• 모든 시간 t에 대해서 \(\hat{y}_t=y_{t-1}\)
• 단기 예측에서는 정확하나 multistep에서는 취약하다.

1. Autoregressive Integrated Moving Average(ARIMA)

• 평균과 분산의 정상성을 이용
• 과거 관측치와 미래 사이에 선형관계가 존재한다고 가정하는 방법

1. Residual-Squeeze Net(RSNet)

• 모델 학습 중 학습된 채널의 최적의 조합을 사용한다.
• RSNet architechture를 사용하는 1-D CNN으로 구성

1. Deep LSTM Encoder-Decoder

• Time-distributed dense layer가 연결된 LSTM layer

1. CNN-LSTM Encoder-Decoder

C. Model Performance Evaluation

• Walf-forward validation 또는 basktesting을 이용하였다.
• k-fold cross validation이나 train-test splitting의 경우 관측 값간에 관계가 없다고 가정하기 때문에 sequential dimension을 보존해야하는 time-series data와는 맞지 않다.
• model evaluation을 위해서는 3가지 error evaluation metrics를 사용하였다.

1) RMSE 2) MAE 3) sMAPE(symmetrical mean absolute percentage error)

\[\begin{aligned} RMSE &= \sqrt{\frac{1}{n}\sum^n_{i=1}(\hat{y}_i-y_i)^2}\\ MAE &= \frac{1}{n}\sum^n_{i=1}|\hat{y}_i-y_i|\\ sMAPE &= \frac{200}{n}\sum^n_{i=1}\frac{|\hat{y}_i-y_i|}{|\hat{y}_i|+|y_i|}. \end{aligned}\]

D. Comparison with Baselines

• 개별적 모델의 성능을 평가하기 위해 window size를 60, 30 두 가지를 section 4-C에서 사용된 evaluation metrics를 사용하여 평가

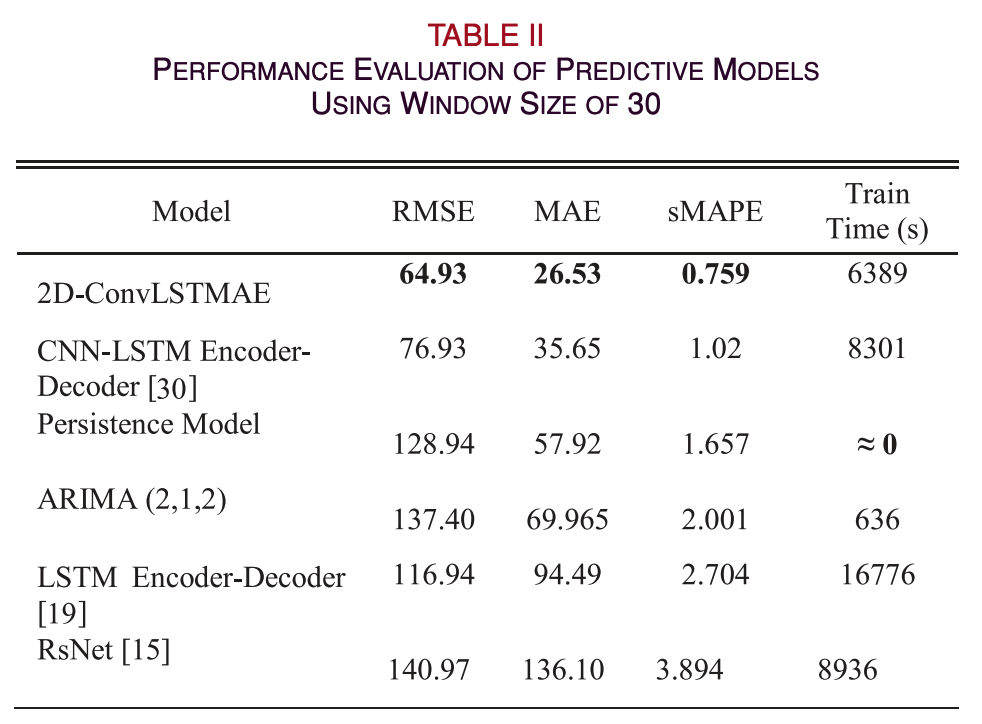
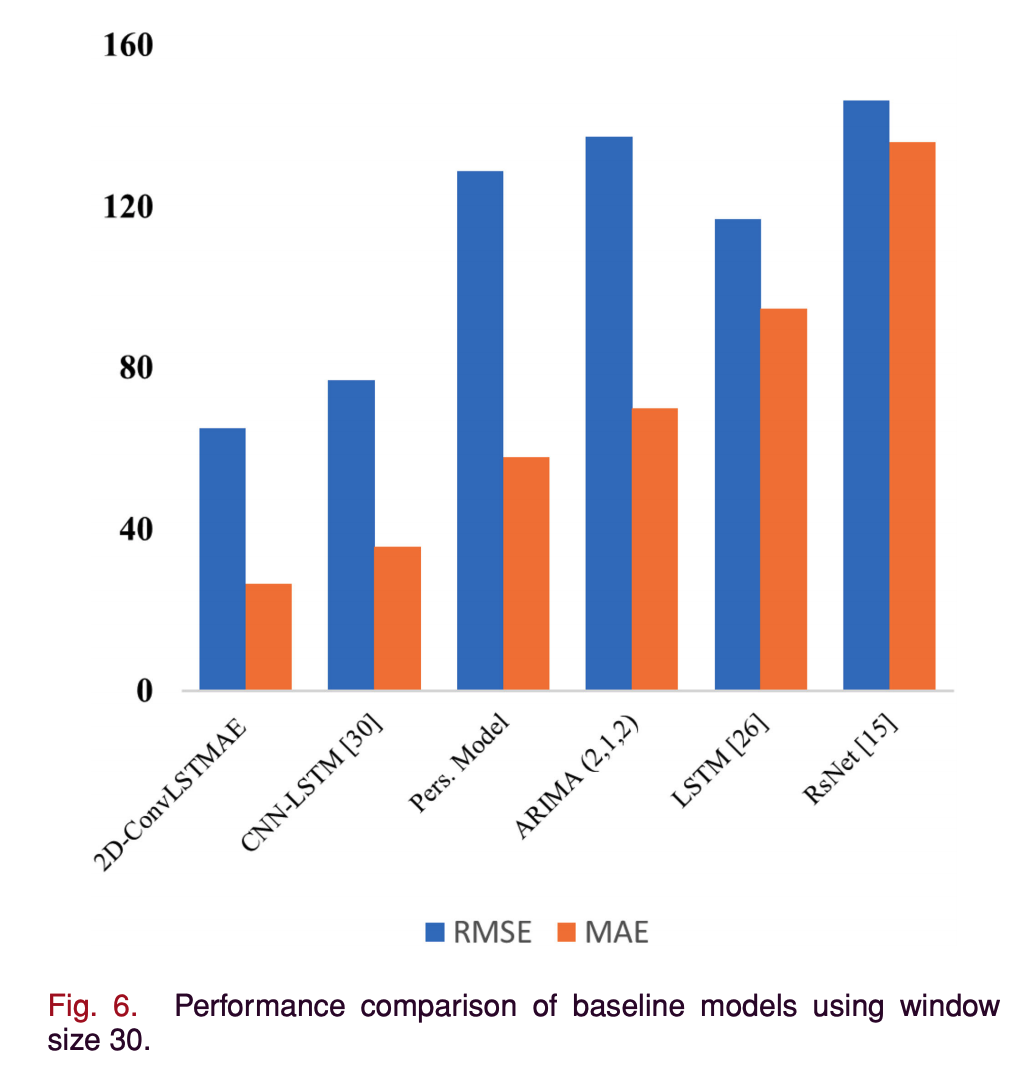
• window size 30의 결과 모든 evaluation metrics에서 2-DConvLSTMAE가 가장 성능이 좋았다.
• 성능외에도 DL 모델 중 가장 학습 속도가 빨랐다.
• ARIMA나 Persistence model이 학습 속도가 더 빠르지만 성능은 나쁘다.
• 보통 Persistence model과 같은 naïve models를 예측 모델의 벤치마크로 사용한다. naïve models보다 성능이 좋은 경우 ‘skillful’하다고 한다.

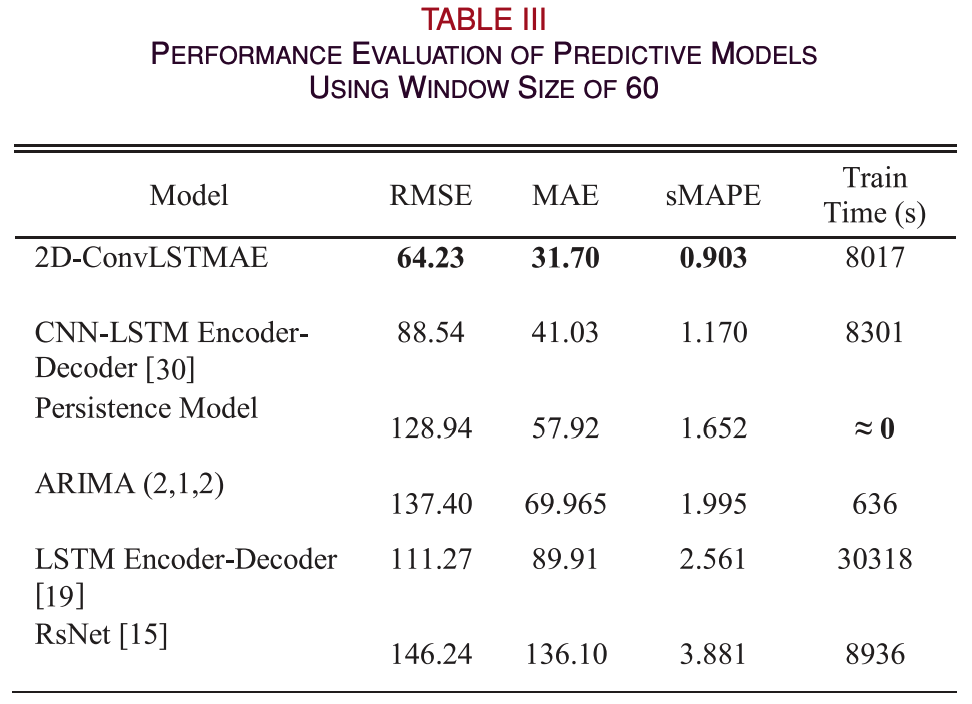
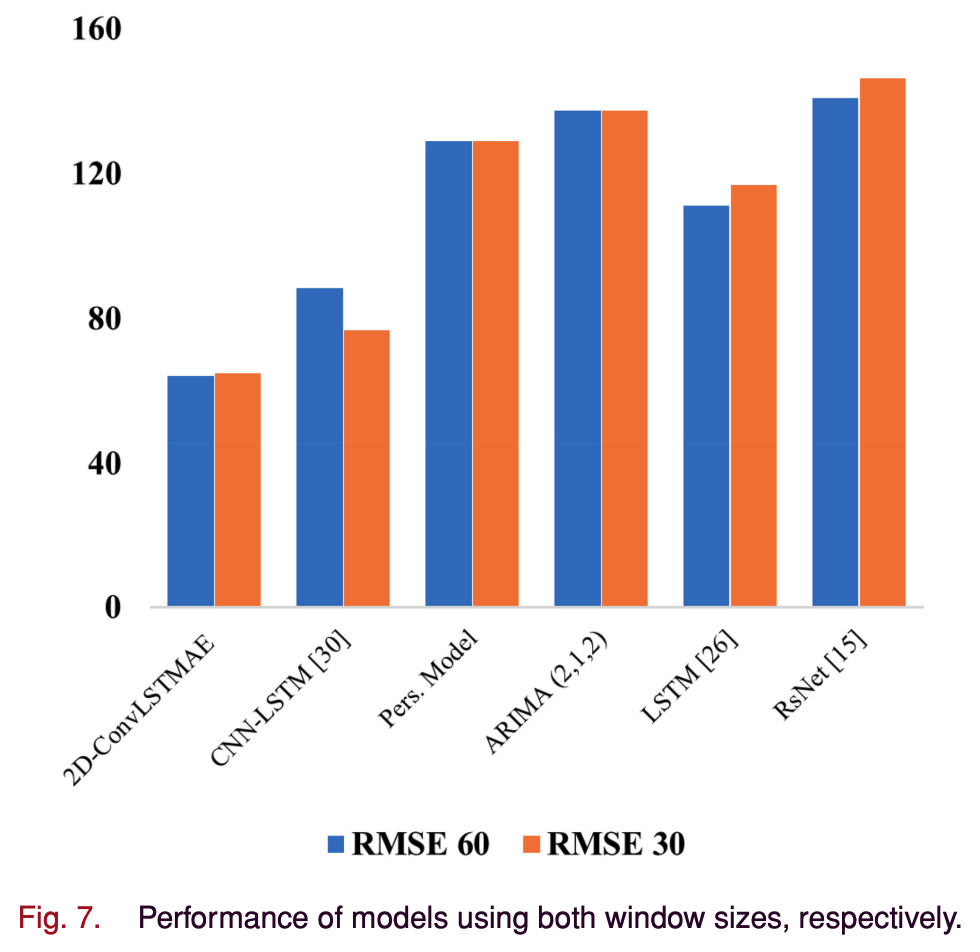
• window size 60의 결과
• ARIMA와 Persistence models의 경우 prior data manipulation이나 transformation이 필요 없다. 따라서 window size에 영향을 받지 않는다.
• 2-DConvLSTMAE가 모든 evaluation metrics에 대해 State-of-the-art DL 모델들보다 성능이 좋다.
• DL baselines와 비교 했을 때 학습시간도 짧다.
• Window size의 변화에도 robustness하다. 하지만 결과를 보았을 때 window size 60이 optimal 하다.

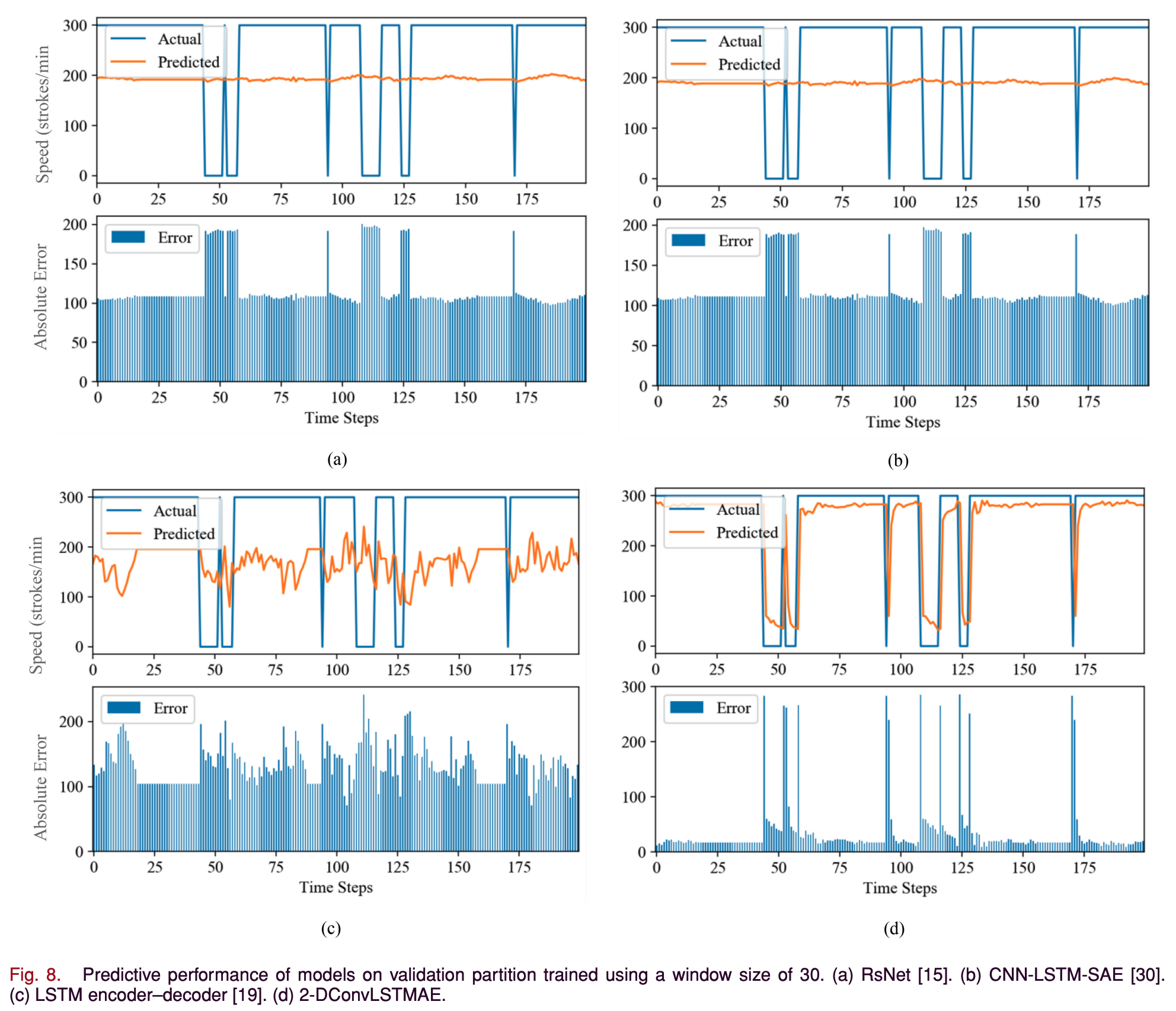
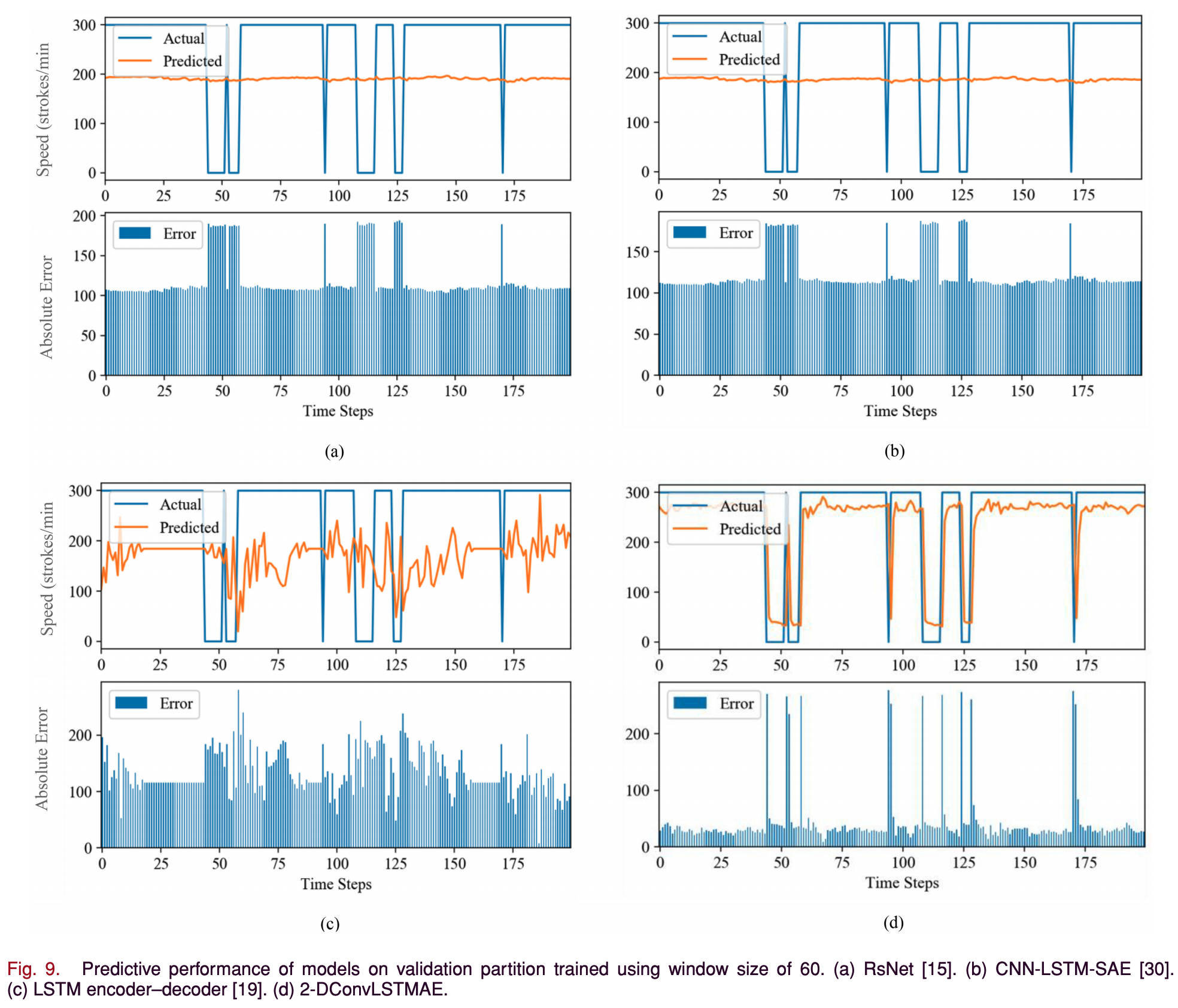
• Figs 8과 9는 window size 30과 60으로 진행하였을 때 첫 200 time steps의 예측 성능을 나타낸다.
• x축은 time steps, y축은 각 subplot에서 위 그래프의 경우 machine speed 아래 그래프의 경우 예측값과 실제값의 absolute error를 나타낸다.
• 2-DConvLSTMAE는 shorther, loger-term window size 모두 SOTA DL 모델들보다 성능이 좋다.
• LSTM encoder-decoder model이 다른 baseline models보다 성능이 더 좋은데 이는 LSTM memory가 long-term dependencies를 더 잘 잡아내기 때문이다.
• 이는 제조 operations large time-series dataset에 ConvLSTM deep networks를 적용할 수 있는 main prospect와 potential를 제공한다.
• 2-DConvLSTMAE의 예측 성능이 기계 속도의 분산과 temporal distribution에 robust하다.

• 2-DConvLSTMAE의 효과는 다음과 같이 설명할 수 있다.

  1. Deep ConvLSTM layers는 LSTM과 CNN models의 장점을 활용하여 sequential data의 공간적, 시간적 분포를 적절하게 캡처한다.

  2. encoder-decoder architechture는 dimensionality reductioin과 비지도 학습 체제로 representation learning을 촉진시켜 model 학습시간을 단축시킨다. encoder-decoder architechture에 ConvLSTM과 LSTM layer를 사용하여 기계 속도 예측에 접근하는 방식의 조합은 기계 속도의 univariate time-series 예측 성능을 높였다.

E. Analysis of Sensitivity of 2-DConvLSTMAE with Respect to Sequence Length

• ConvLSTM의 sequence 길이는 최적화해야하는 hyperparmeter이다.
• 이 모델은 p subsequences로 더 세분화 하였다.
• subsequences는 \(l-\frac{w}{p}\)와 같은 uniform length를 갖는다. (\(l\) : subsequences length, \(w\) : window size)
• 최적의 l을 얻기 위해 hyperparmeter의 민감도를 분석한다.
• subsequences의 길이를 60,30,20,12,10으로 설정하고 predictive error와 학습 시간에 미치는 영향을 테스트한다.

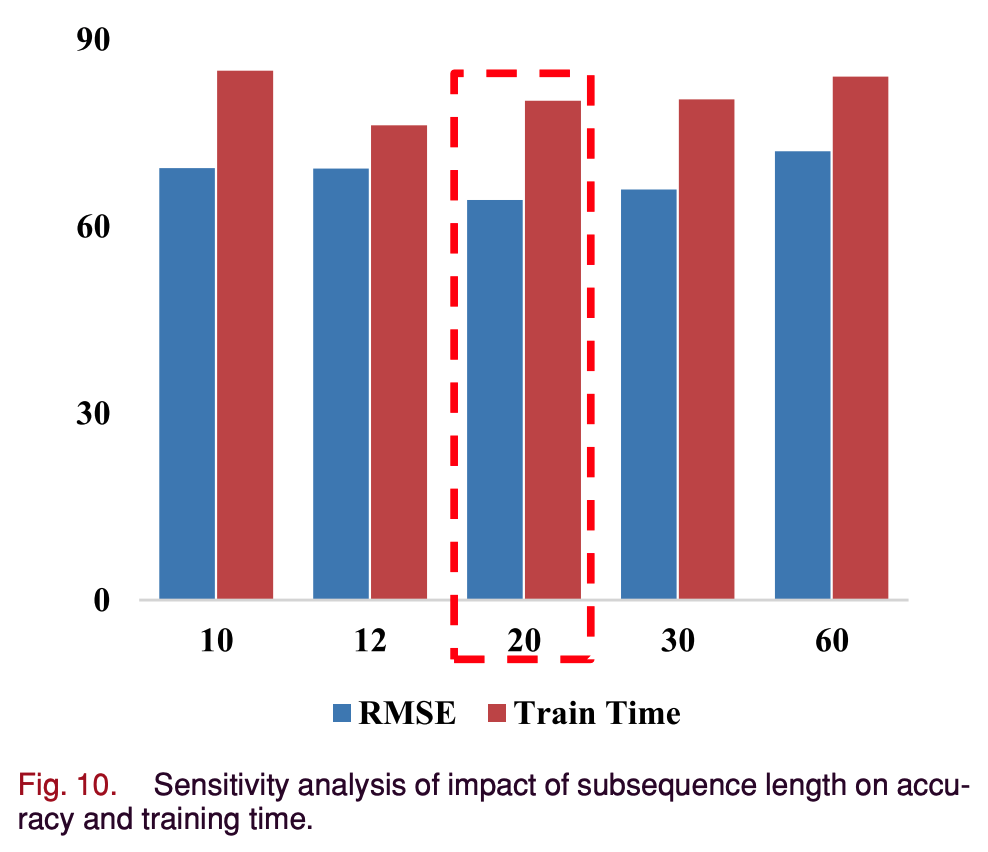
• 그림 10은 subsequences의 길이가 다른 2-DConvLSTMAE의 성능 결과이다.
• 최적 I는 20으로 RMSE와 훈련 시간이 가장 짧다.
• 최적의 sequence의 길이는 개별 생산 주기 및 다양한 데이터 분포에 연결될 수 있는 특정 애플리케이션에 따라 달라질 수 있다.

Conclusion

• 스마트 제조 공정에서 기계 속도 예측을 위해 새로운 Deep ConvLSTM autoencoder architechture를 제안
• sliding window approch를 사용하여 입력 sequence를 지도 학습 방식으로 재구성하여 multistep time-series 예측 문제에 적용하였다.
• CNN과 LSTM을 합쳐 CNN의 장점인 automatic feature extraction과 LSTM의 sequential, representation learning을 활용하였다.
• encoder-decoder architechture는 representation learning을 촉진시켜 computational demand와 학습시간을 줄였다.

분석의 결과로는

1) 2-DConvLSTMAE는 naïve and statistical bench mark models와 state-of-the-art DL time-series models보다 향상된 예측 성능

2) 훨씬 더 적은 학습 시간을 필요로 한다. 이로 인해 기계 속도 예측이 향상될 뿐 아니라 실제 제조 공정에서 채택하기 위한 실용적인 접근 방식이라고 할 수 있다.

이 논문에서 얻은 결과를 스마트 제조 프로세스 운영을 위한 multistpe time-series 예측에 직접 적용하여 생산 일정 및 계획을 개선 할 수 있다. 예를 들어, 기계 속도를 미리 예측하는 것은 운영 요구 사항을 적절하게 조정할 수 있도록 향후 생산 출력을 표시함으로써 적시 생산을 촉진하는 데 사용할 수 있다. 이 논문의 향후 확장에는 제안된 모델을 기계 상태 및 외부 센서 데이터를 포함한 다변량 시계열로 확장하는 것이다.