USAD : UnSupervised Anomaly Detection on Multivariate Time Series

Published: Feb 15, 2021 by Dev-hwon

USAD : UnSupervised Anomaly Detection on Multivariate Time Series Julien Audibert, Pietro Michiardi, Frédéric Guyard, Sébastien Marti, Maria A. Zuluaga, KDD 2020

논문을 읽고 고려대학교 산업경영공학부 DSBA 연구실 최희정 선배님의 세미나 발표 자료를 참고하였습니다.

USAD : UnSupervised Anomaly Detection on Multivariate Time Series

차별점 : 결과가 좋은 여러 기법들이 존재하지만, 수행 기준에서 training time(i.e. energy consumption)을 고려하지 않는다.

Problem formulation

Dataset : set of multivariate time series

\[\mathscr{T}=\left \{ \textbf{x}_1, \dots, \textbf{x}_T \right \}, \;\;\textbf{x}\in \mathbb{R}^m\]

window : 길이가 k인 time window

\[W_t=\left \{ \textbf{x}_{t-K+1}, \dots, \textbf{x}_{t-1}, \textbf{x}_t \right \}\]

time window를 input으로 t시점의 normal/abnormal 여부를 예측

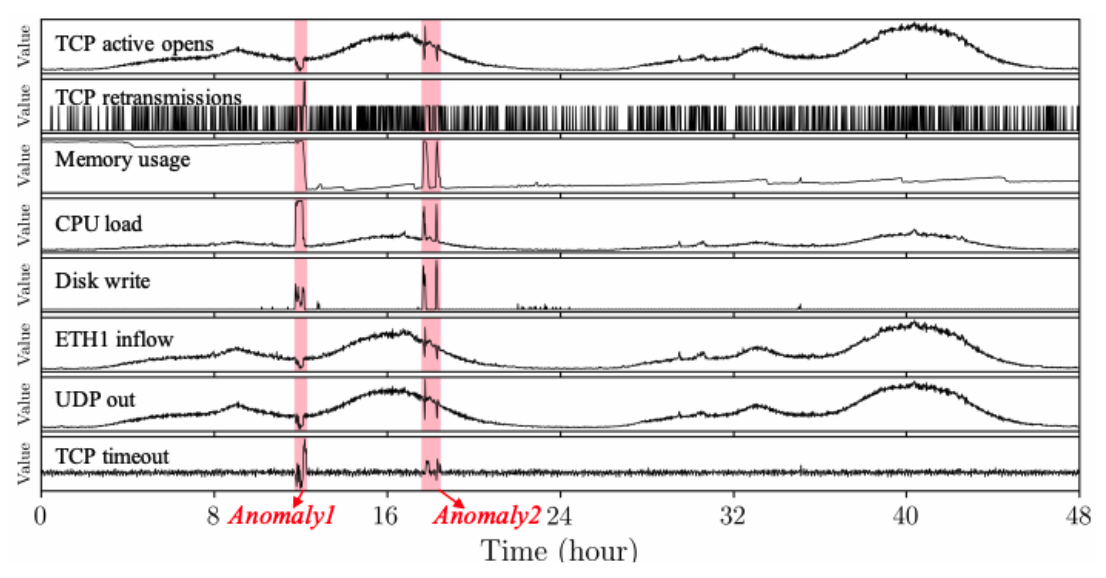
Unsupervised Anomaly Detection

AE-based multivariate time series AD

Autoencoder 구조인 Encoder \(E\)와 Decoder \(D\)를 이용
original input vector \(X\)와 reconstruction \(R\)의 차이인 reconstruction error를 최소화
정상데이터의 reconstruction error를 기반으로 학습하여 정상 데이터의 분포를 학습함
reconstruction error를 anomaly scores로 사용, threshold를 초과하면 이상치로 탐지함

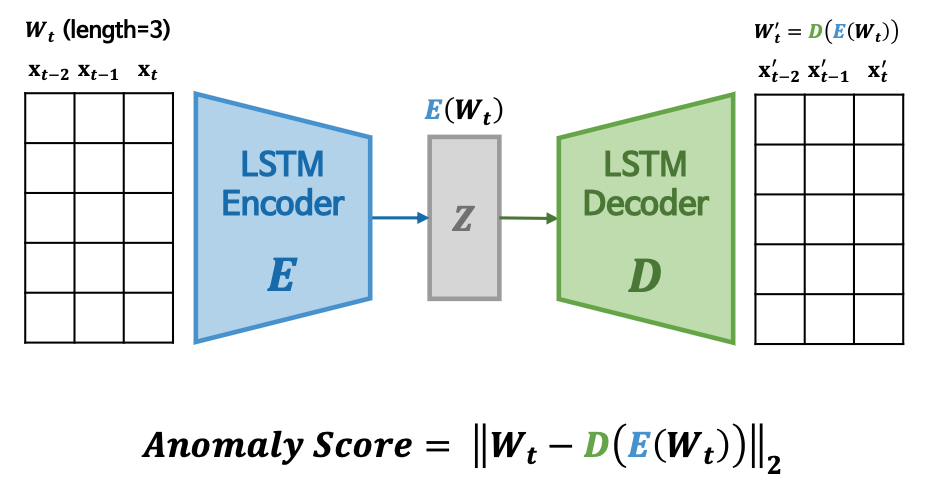
\[\begin{matrix} \text{as:} & \\ & \;\;\;\;\;\;\; \mathscr{L}_{AE}=\left \| X-AE(X) \right \|_2,\\ \text{where} & \\ & \;\;\;\;\;\;\; AE(X)=D(Z), \;\;\; Z=E(X)\\ \end{matrix}\] \[\text{and } \left \| \cdot \right \|_2 \text{ denotes the L2-norm.}\]

단점: anomaly가 매우 작은 경우, normal data와 근접하는 경우에 reconstruction error가 매우 작아 detection이 잘 안됨.

GAN-based multivariate time series AD

GAN을 이용하여 anomaly detection 하는 방법
generator와 discriminator 두 개의 모델을 이용하여 generator는 실제와 비슷하게 samples를 생성하여 discriminator를 속이고 discriminator는 generator가 만든 가짜를 찾아내는 방법
GAN-AD에 대해서는 저번 포스트에서 자세하게 다뤘으니 참고할 것 포스트 보러가기

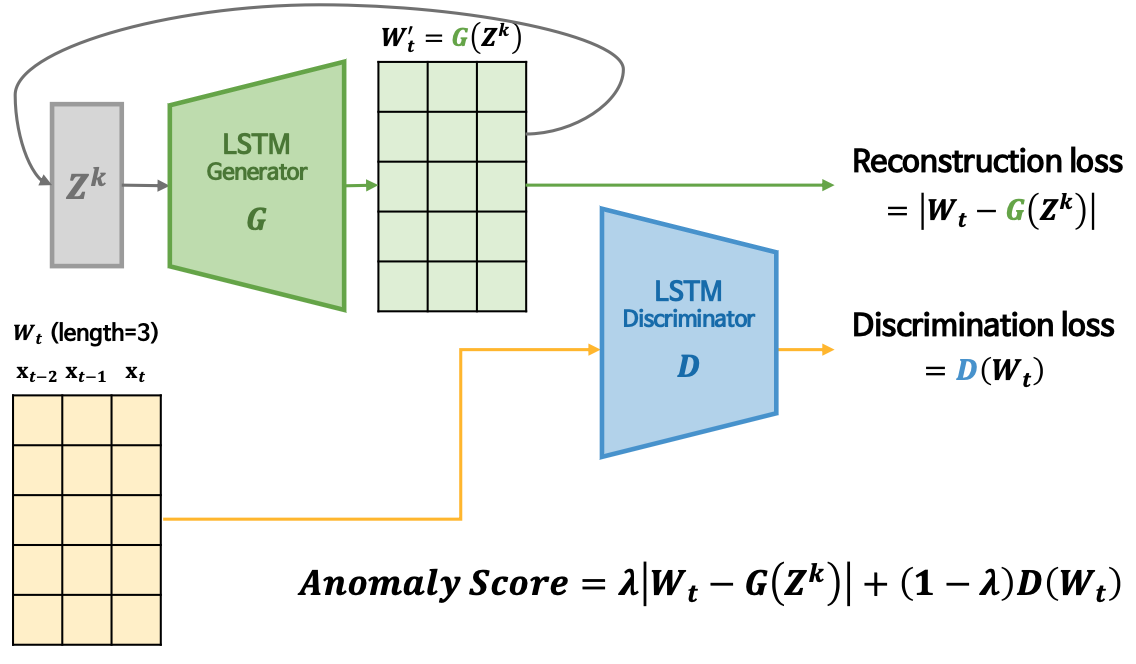
학습이 불안정하여 mode collapse, non-convergence 문제가 존재

Unsupervised Anomaly Detection(USAD)

두 단계의 Adversarial training framework 내의 AE 아키텍처 이용
세가지 elements로 구성
- encoder network \(E\), two decoder networks \(D_1, \;D_2\)

\[AE_1(W)=D_1(E(W)), \;\; AE_2(W)=D_2(E(W))\]

1) 두 AE가 normal input windows W를 재구축하게 학습 2) 두 AE가 adversarial하게 학습, \(AE_1\)은 \(AE_2\)를 속이게 학습하고, \(AE_2\)는 실제 데이터와 \(AE_1\)으로부터 재구축된 데이터 구별하게 학습

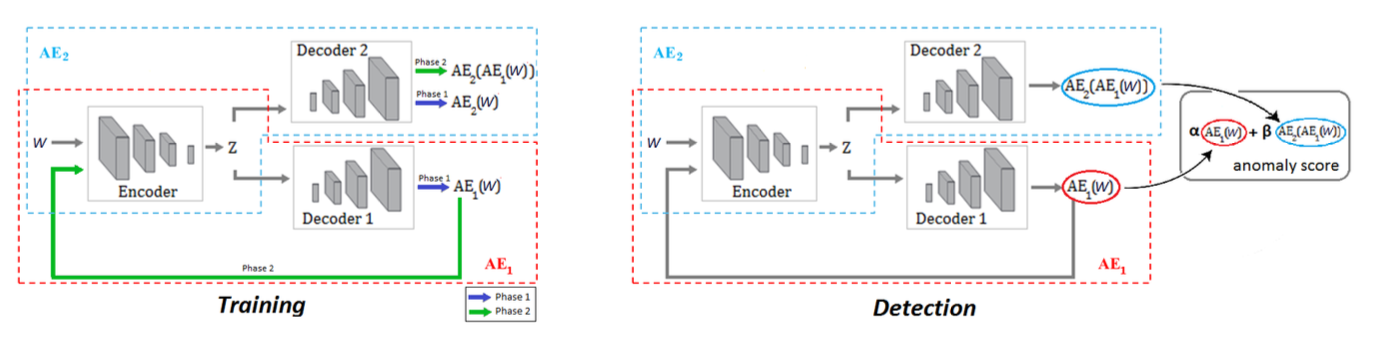
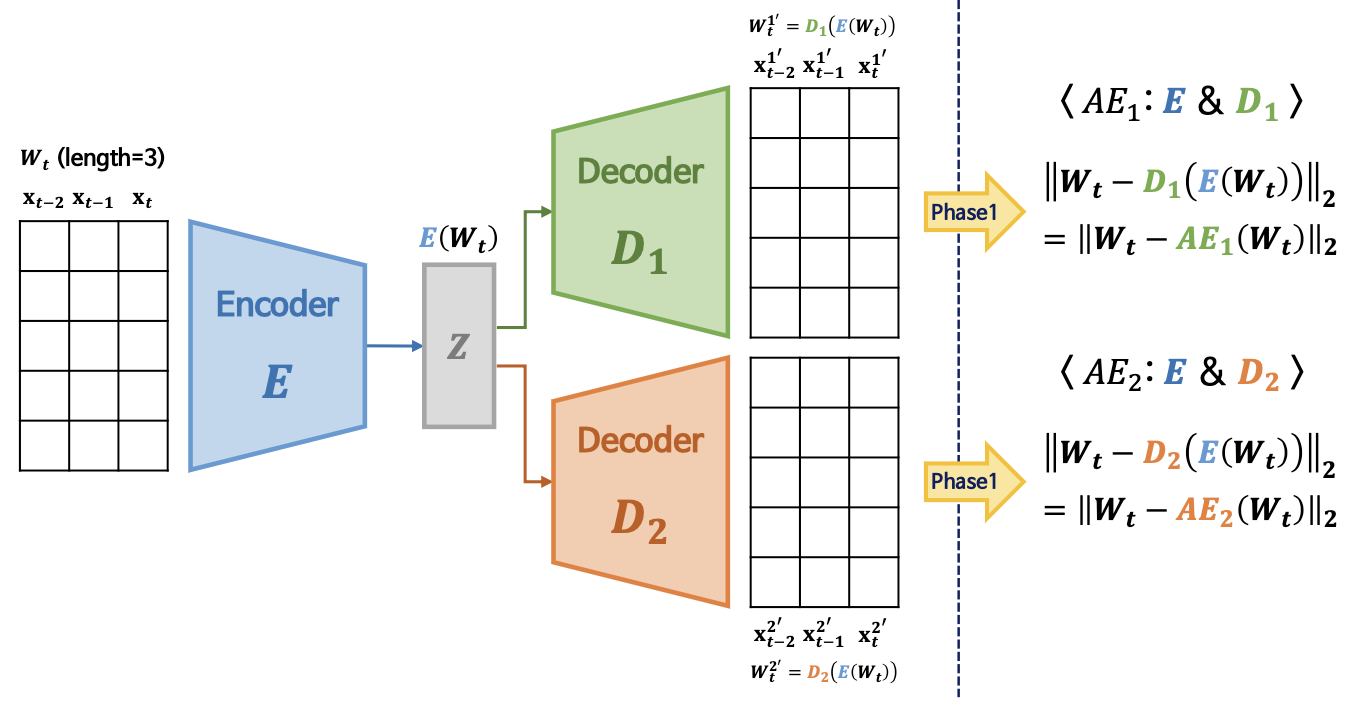
Phase 1. Autoencoder training

Input data W를 encoder E를 이용하여 latent space Z로 압축, 각 decoder로 재구축하게 학습
이때, adversarial training을 위해 Encoder 𝑬, Decoder 𝑫𝟏, Decoder 𝑫𝟐를 기반으로 encoder를 공유하는 두 개의 AE를 구축함

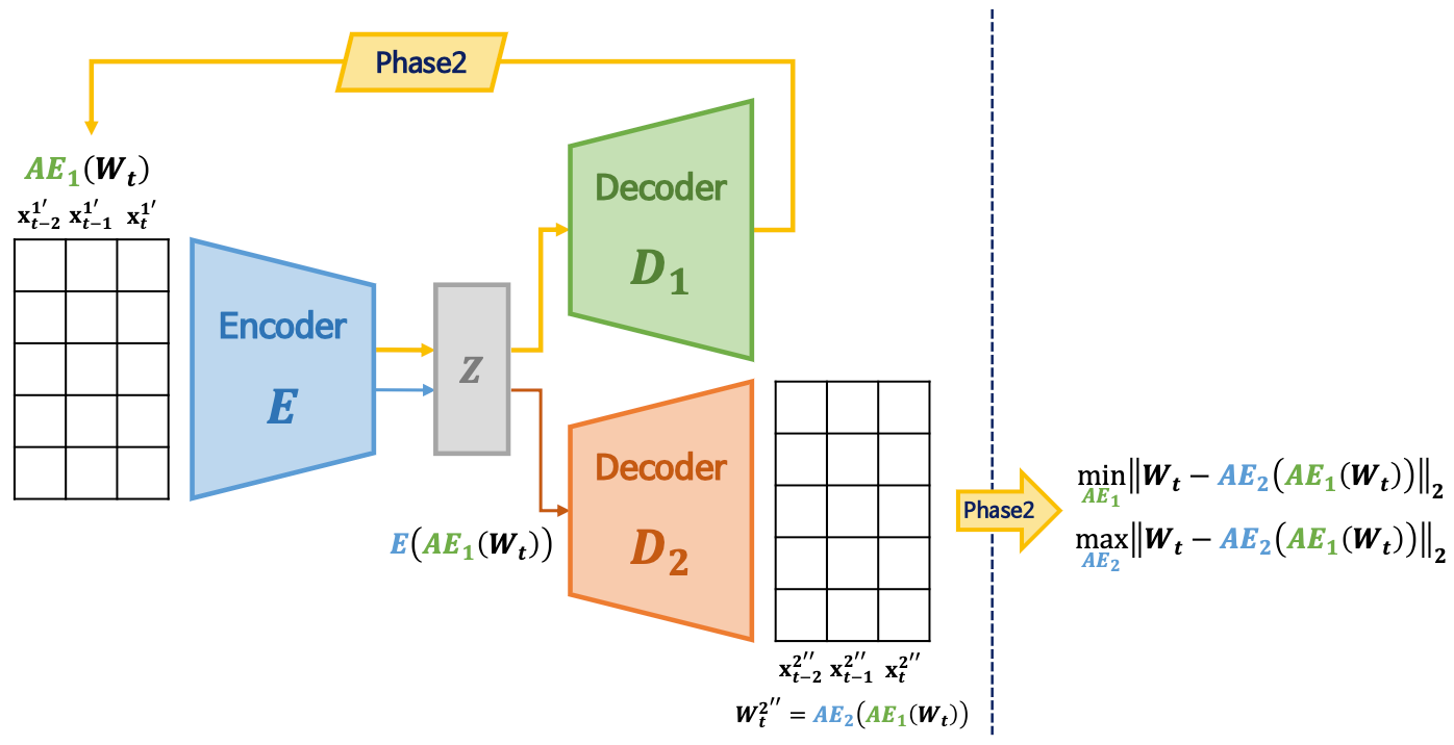
\[\begin{matrix} \mathscr{L}_{AE_1} = \left \| W-AE_1(W) \right \|_2 \\ \mathscr{L}_{AE_2} = \left \| W-AE_2(W) \right \|_2 \\ \end{matrix}\]

Phase 2. Adverserial training

\(AE_2\)는 실제 데이터와 \(AE_1\)이 만든 데이터 구별하게 학습
\(AE_1\)는 \(AE_2\)를 속이게 학습

\[\underset{AE_1}{\text{min}}\underset{AE_2}{\text{max}}\left \| W-AE_2(AE_1(W)) \right \|_2\]

Two-phase training

USAD를 구성하는 두 AE의 학습목표는 다음과 같음
- \(AE_1\): input을 잘 복원하면서 \(AE_2\)를 잘 속이는 모델 학습
- \(AE_2\): input을 잘 복원하면서 \(AE_1\)이 복원한 데이터와 input을 잘 구별하는 모델 학습
\(AE_2\) 도입 및 adversarial training을 통해 정상 데이터와 유사한 이상치를 탐지하는 것을 가능하게 하며, AE 구조를 통해 안정적인 학습이 가능하게 함

\[\begin{matrix} \mathscr{L}_{AE_1}=\frac{1}{n}\left \| W-AE_1(W) \right \|_2 + (1-\frac{1}{n})\left \| W-AE_2(AE_1(W)) \right \|_2 \\ \mathscr{L}_{AE_2}=\frac{1}{n}\left \| W-AE_2(W) \right \|_2 - (1-\frac{1}{n})\left \| W-AE_2(AE_1(W)) \right \|_2 \end{matrix}\]

n은 epoch
안정적인 학습을 위해 초반에는 reconstruction에 가중치를 주고, 후반에는 adversarial training에 가중치 부여

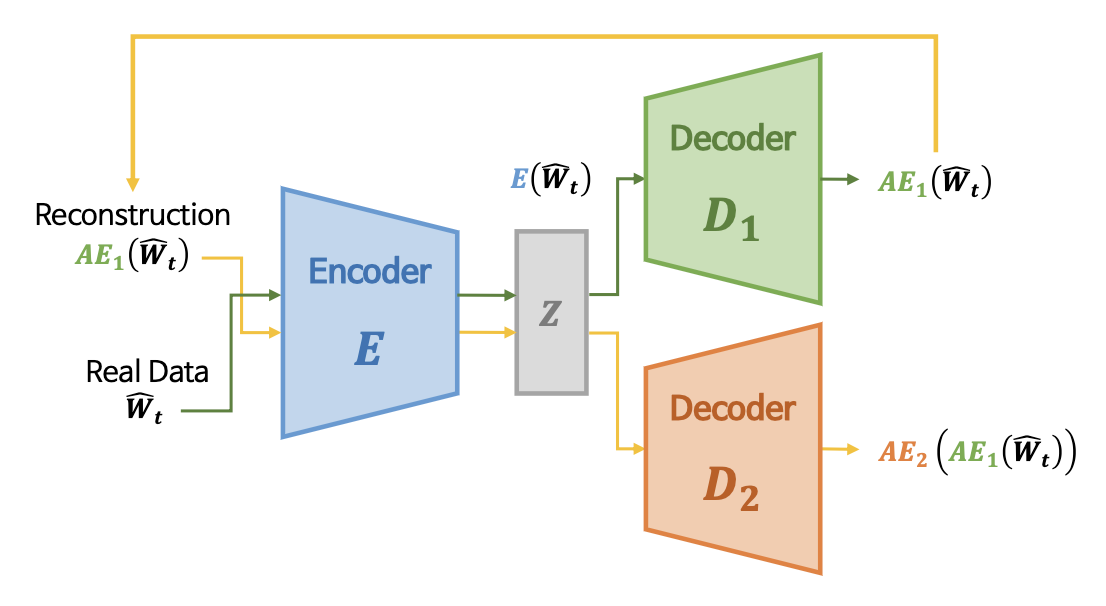
Inference

anomaly score
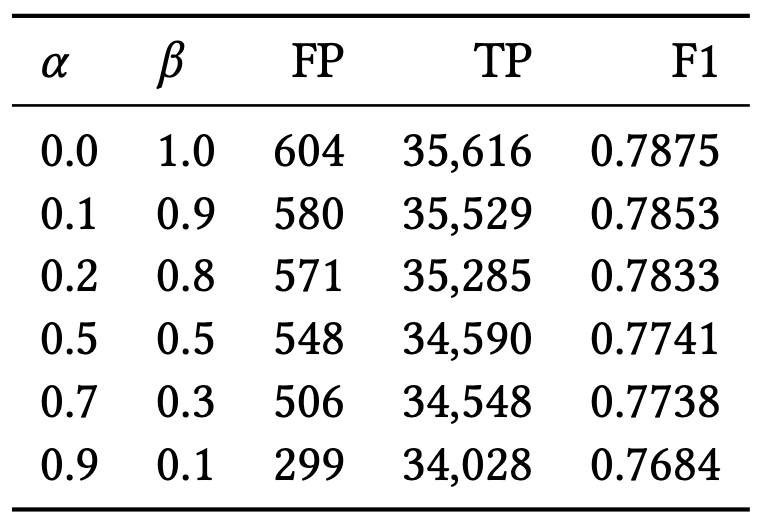
- 학습이 완료된 두 AE를 기반으로 아래와 같이 anomaly score를 산출함 \(\mathscr{A}(\hat{W})=\alpha\left \| \hat{W} - AE_1(\hat{W}) \right \|_2+\beta\left \| \hat{W} - AE_2(AE_1(\hat{W})) \right \|_2\)
- \[\alpha+\beta=1\]
- 계수의 비중에 따라 아래와 같이 false positive와 true positive 간의 trade-off가 발생함
  - 𝜶 > 𝜷: true & false positive 감소 → low detection sensitivity scenario
  - 𝜶 < 𝜷: true & false positive 증가 → high detection sensitivity scenario

		True	True
		Abnormal	Normal
Predicted	Abnormal	True Positive	False Positive
Predicted	Normal	False Negative	True Negative

Experiments and results

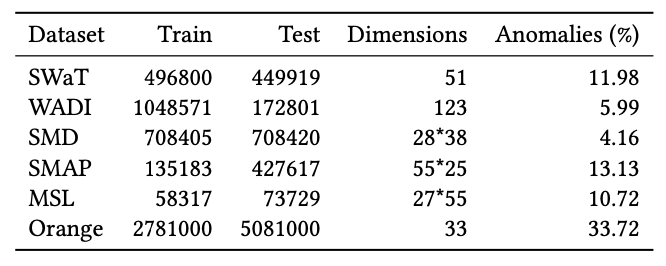
Datasets

5개의 publicly available datasets과 1개의 internal dataset으로 결과를 냄
Window 내부의 한 시점이라도 abnormal이면 해당 구간의 ground truth를 abnormal로 부여하는 point-adjust 방식을 통해 모델의 성능을 평가함

Evaluation Metrics

Precision(\(P\)), Recall(\(R\)), F1 score(\(F1\)), average precision과 average recall을 이용하여 계산한 F1 score(\(F1^*\)) 사용하여 평가

\[P=\frac{TP}{TP+FP}, \;\; R=\frac{TP}{TP+FN}, \;\; F1=2\cdot\frac{P\cdot R}{P+R}, \;\; F1^*=2\cdot\frac{\bar{P}\cdot \bar{R}}{\bar{P}+\bar{R}}\]

Baselines

5개의 baselines를 이용하여 비교

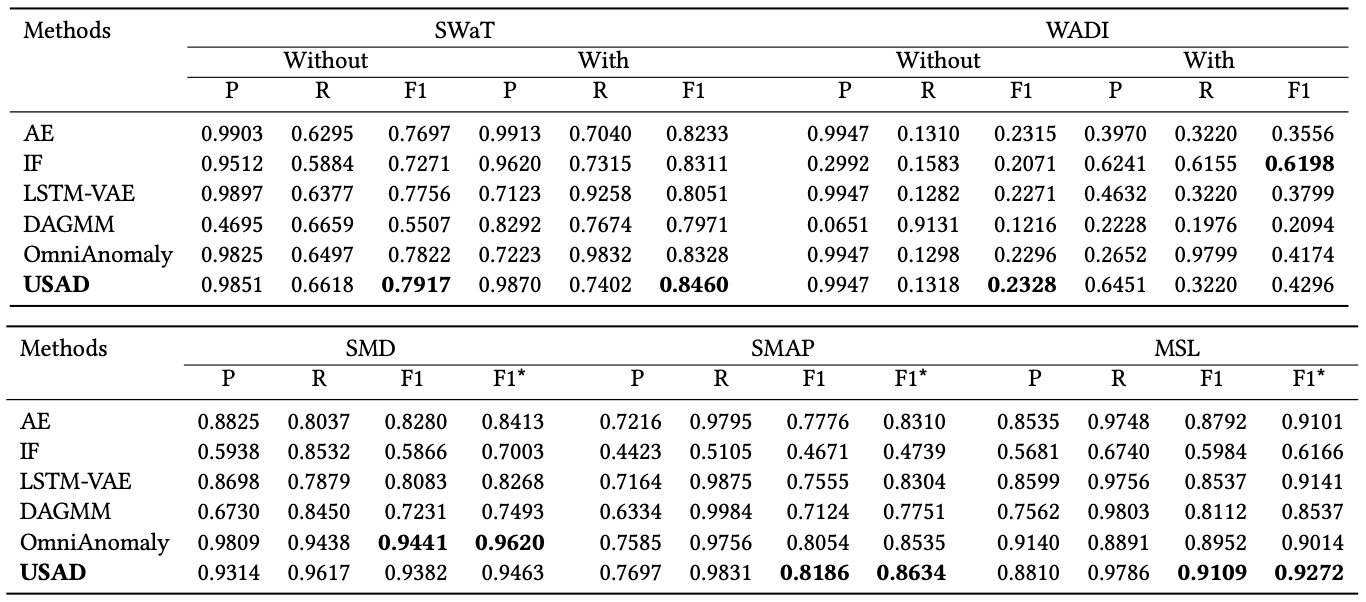
Overall performance

제안한 방법론이 대부분의 데이터에서 우수한 성능을 도출함
시계열 정보를 사용하지 않은 IF와 DAGMM이 낮은 성능을 도출하는 것을 통해 temporal information을 모델링하는 것이 중요함을 알 수 있음

Effect of parameters

SWaT dataset을 기반으로 총 4개의 parameter가 모델에 미치는 영향을 확인함
- Down-sampling: 데이터를 샘플링하는 주기
- Windows size: input의 sequence 길이
- Dimension of latent space: AE의 latent space 차원
- Percentage of anomalies: train dataset에 포함되는 anomaly 비율
Down-sampling값이 5일때 최고 성능을 도출하며,비율의 값에 관계 없이 일정한 성능을 도출하는 것을 통해 모델이 down-sampling에 민감하지 않음을 알 수 있음
Window size가 10일때 최고 성능을 도출하는 것을 통해 각 시점이 이상치 탐지에 큰 영향을 미치고 USAD가 이상치를 빠르게 탐지할 수 있다고 볼 수 있음

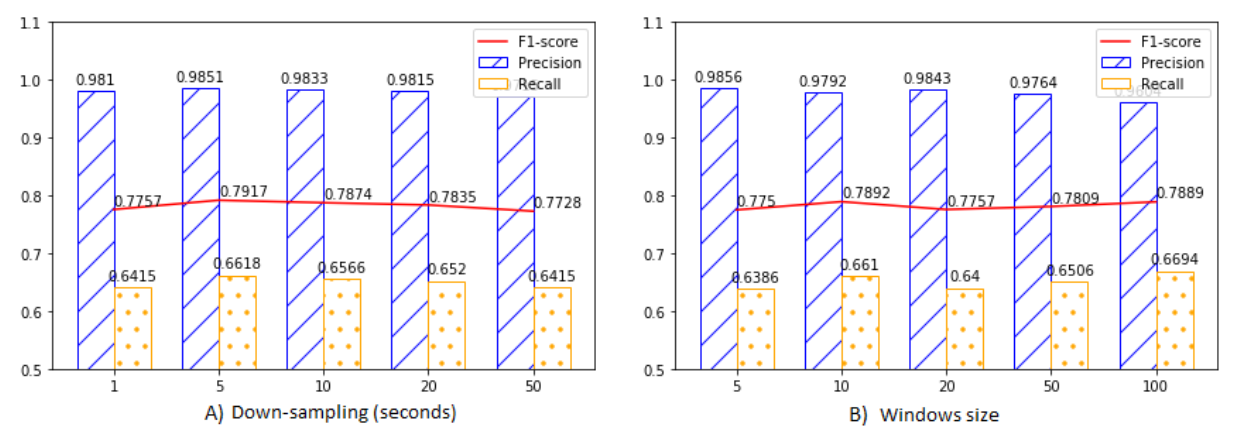
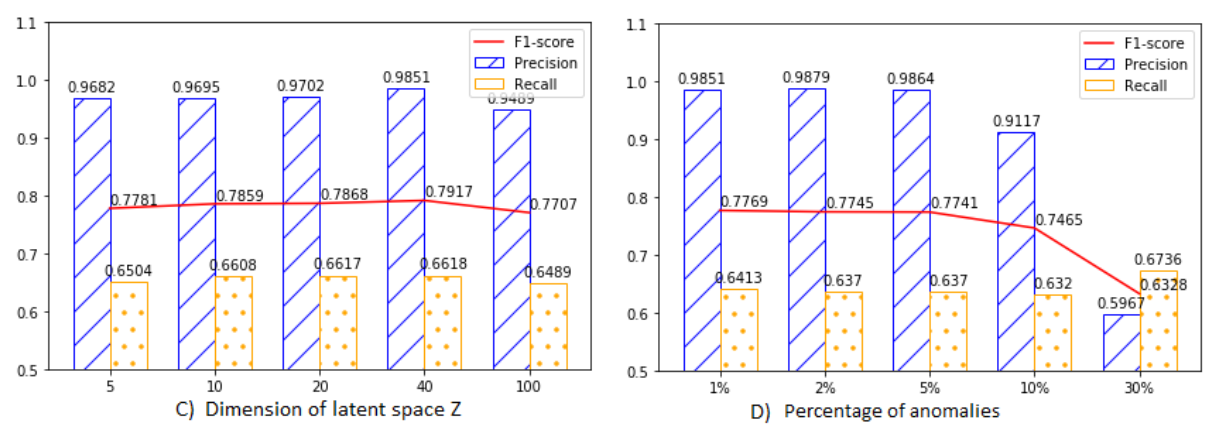
Dimension of latent space가 20일 때 최고 성능을 도출하며, 값이 작을 때는 정보 손실이 발생하고 클 때는 memorization이 발생해 성능이 낮은 것을 확인할 수 있음
Training data의 percentage of anomalies가 증가함에 따라 precision이 크게 감소하는 것을 통해 false positive가 증가함을 알 수 있음

anomalyscore의 parameter 𝜶와 𝜷의 값에따라 상이한 결과가 도출되는 것을 통해 모델이 𝜶와 𝜷에 민감함을 알 수 있으며, 𝜶가 증가하고 𝜷가 감소할수록 false positive와 true positive가 모두 감소하는 것을 확인할 수 있음

Ablation Study

SMD, SMAP, MSL datasets을 기반으로 2개의 phase의 효과를 검증
Adversarial training의 접목이 AE의 성능을 유의미하게 향상시키는 것을 통해 adversarial training이 정상 데이터와 유사한 이상치를 탐지하는데 도움이 된다고 볼 수 있음

Feasibility Study

실제현장에서 사용되는 internal dataset을 기반으로 제안한 모델의 feasibility를 검증한 결과 이상치 탐지 성능이 우수한것을 확인함