Published: Aug 21, 2021 by Dev-hwon
이 내용은 고려대학교 강필성 교수님의 Business Analytics 수업을 보고 정리한 것입니다.
아래 이미지 클릭 시 강의 영상 Youtube URL로 넘어갑니다.
Parzen Window Density Estimation
1. Kernel-density Estimation
밀도 자체를 특정한 분포로부터 생성되었다고 가정하고 어떠한 형태의 사전에 정의된 분포가 아닌 데이터들로 부터 개별 데이터가 발생할 확률을 추정 (non-parametric density estimation)
- 1-D example
- 분포 \(p(x)\)에서 추출한 벡터 \(x\)가 표본 공간의 주어진 영역 \(R\)에 속할 확률
\(P=\int_R p(x')dx'\) 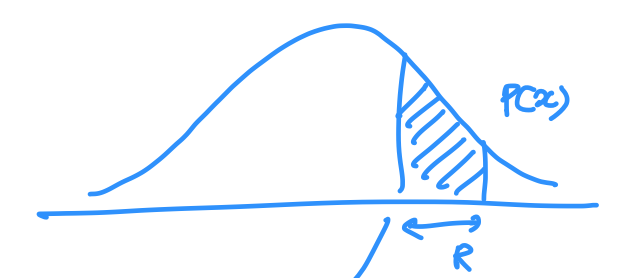
- N개의 벡터 \(\{x^1,x^2,\cdots,x^n\}\)이 분포에서 추출된다고 가정. N개의 벡터 중 \(k\)가 \(R\)에 속할 확률은 다음과 같다.
- \(k/N\)의 평균과 분산
- \(N\)을 \(\infty\)만큼 샘플링을 수행하면, 분산은 거의 0에 가까워질 것이고, 확률 \(P\)는 원하는 영역 안에 들어오는 객체 수로 근사가 가능할 것이다.
- \(R\)이 매우 충분히 작은 영역이어서 \(p(x)\)가 급격하게 바뀌지 않는다고 할 수 있다면,

- 위 두 결과를 합치면,
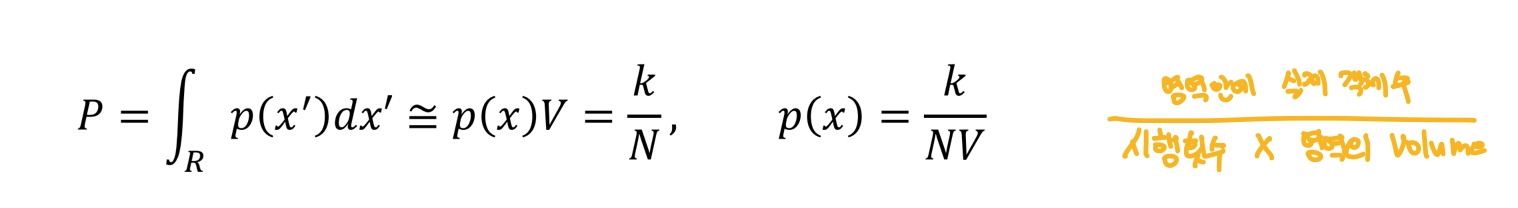
이렇게 확률 밀도를 어떠한 분포로 가정하지 않고, 현재 가지고 있는 데이터와 보고자 하는 영역의 크기, 영역안에 존재하는 데이터의 갯수로 근사하겠다는 것이 Kernel-density Estimation의 목적
✓ 특징
- sample points \(N\)이 커질수록, volume \(V\)가 작을수록 정확해진다. (volume이 작아야지만 volume 내에 확률 밀도 함수 값이 균일하다는 가정을 만족하기 쉽다.)
- 보통 \(N\)은 고정, \(V\)를 찾는 문제
- 충분한 example을 포함할 만큼 \(R\)은 커야하고,
- \(p(x)\)는 영역 \(R\)안에서는 일정하다는 가정을 만족할 만큼 작아야 한다.
- \(V\)를 고정하고 \(k\)를 찾는 문제 : Kernel-density estimation
- \(k\)를 고정하고 \(V\)를 찾는 문제 : k-nearest neighbor density estimation
2. Parzen Window Density Estimation
- \(k\)개의 example을 둘러싸는 영역 \(R\)이 \(x\)를 중심으로 하는 길이 \(h\)의 변을 갖는 hypercube라고 가정
- \(V=h^d, \; d: N\).dimension
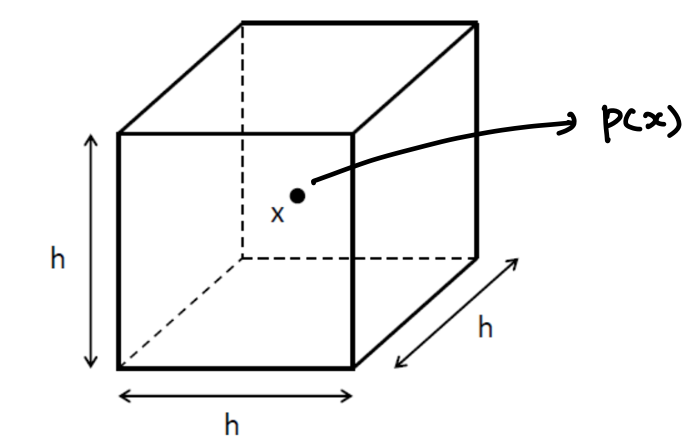
- Kernel function \(K(u)\)

- 예) 빨간색의 \(k, \;p(s)\)
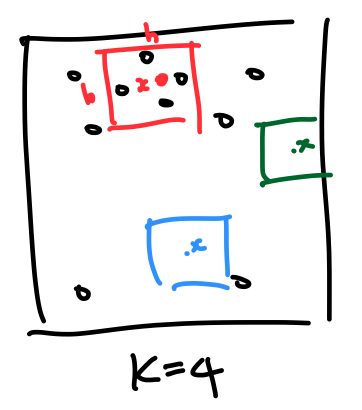
✓ Drawbacks of \(K(u)\)
- Yields density estimate that have discontinuities
- estimation point \(x\)까지의 거리에 관계없이 모든 점 \(x_i\) 에 균등하게 가중치를 부여
✓ Smooth kernel function
Drawback 문제 완화
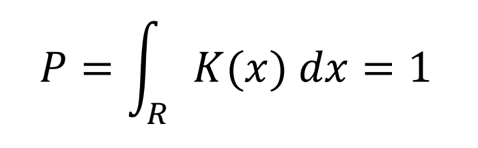
일반적으로 gaussian과 같은 radially symmetric 및 unimodal pdf를 사용

개별적인 객체를 gaussian distribution의 중심으로 보고 그 중심으로 부터 얼마만큼 떨어져있는지에 대한 확률값을 개별적으로 계산하여 확률 밀도 값을 추정
✓ Example of smooth kernels (참고)
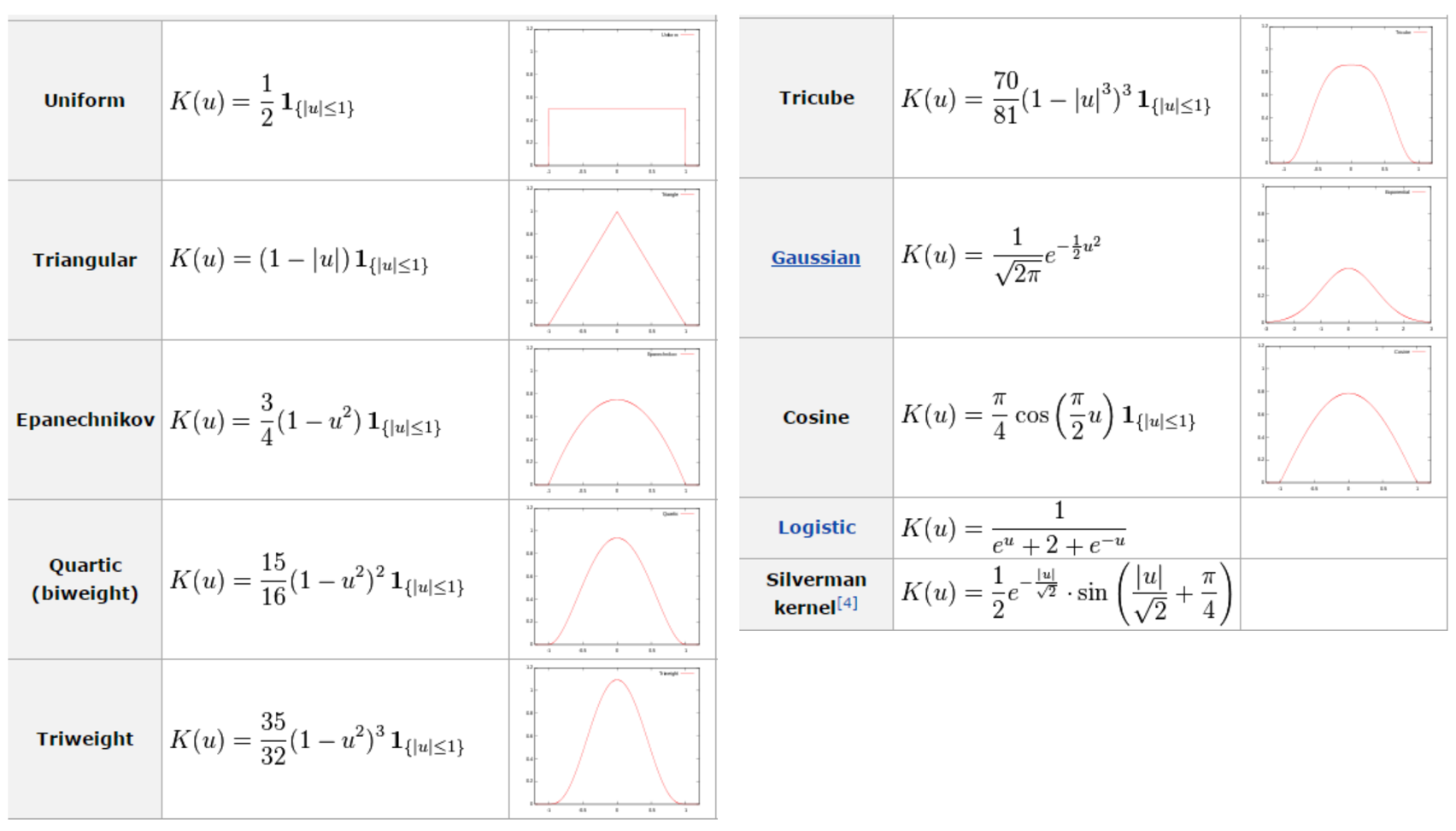
✓ Smoothing parameter (bandwidth) \(h\)
- \(h\)가 너무 크면, 원래 밀도 함수의 over-smooth
- \(h\)가 너무 작으면, 봉우리가 뾰족 (spiky density distribution)
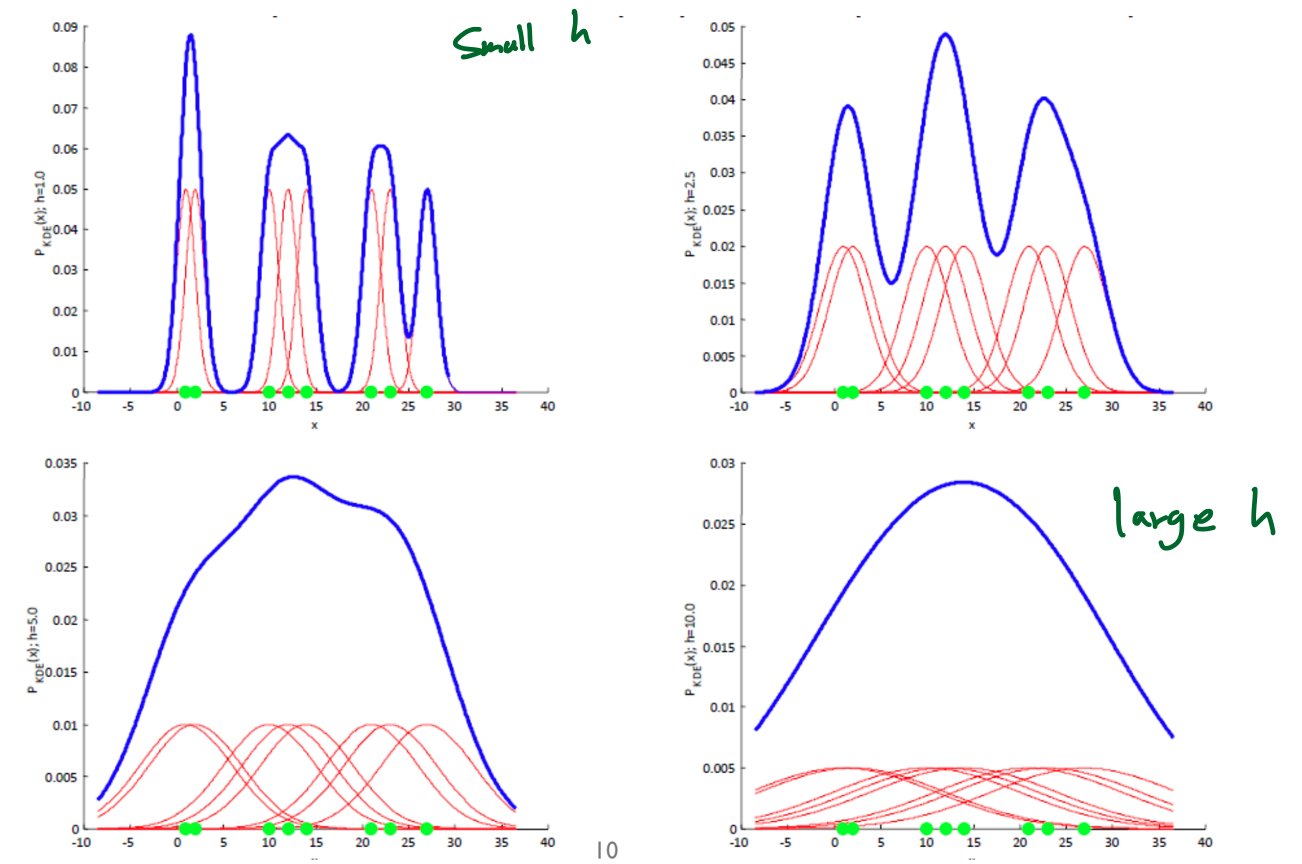
likelihood를 최대화 할 수 있는 bandwidth를 찾아가는 것이 parzen window density estimation의 학습과정의 필요한 절차
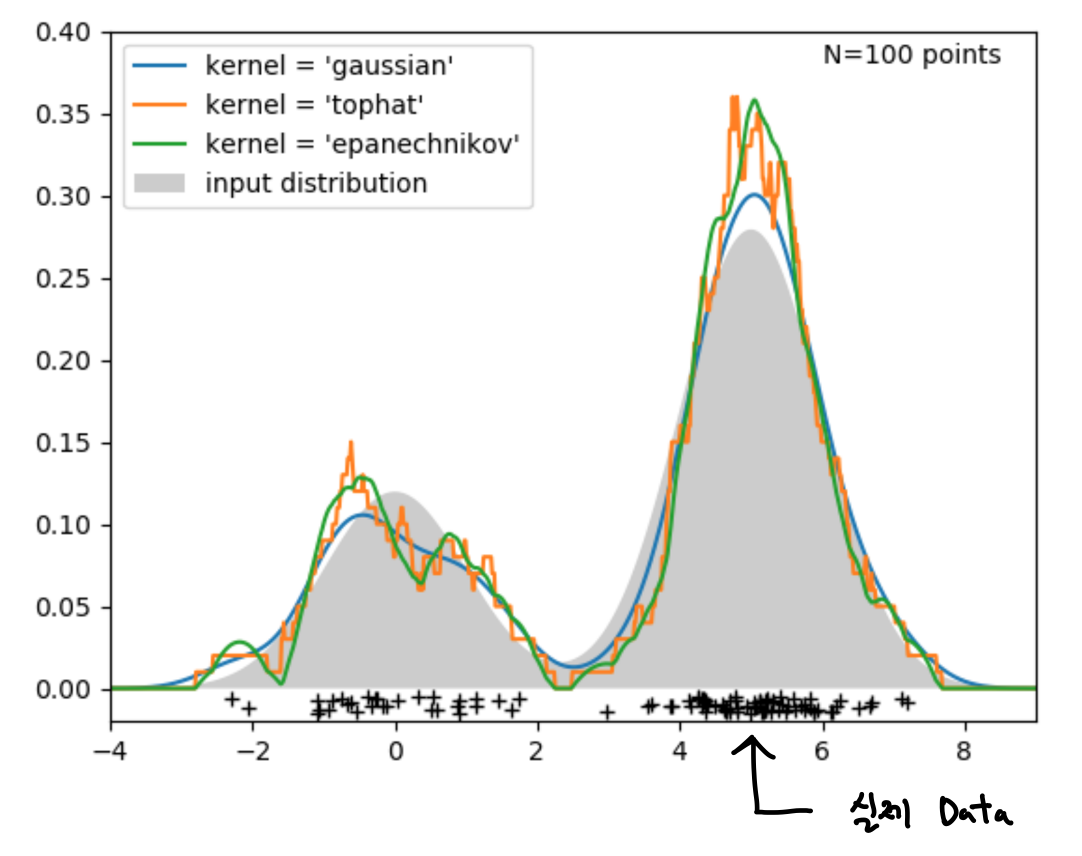
✓ 비교




