Published: Aug 20, 2021 by Dev-hwon

이 내용은 고려대학교 강필성 교수님의 Business Analytics 수업을 보고 정리한 것입니다.

아래 이미지 클릭 시 강의 영상 Youtube URL로 넘어갑니다.

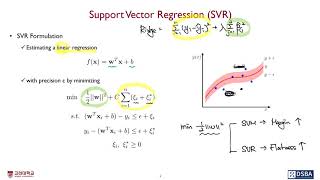
Support Vector Regression

예측하고자 하는 변수가 연속형 수치형 변수

loss function과 flatness라고 하는 모형의 단순성을 하나의 목적함수로 결합

1. \(\varepsilon\)-SVR

✓ Loss function

• 기본적인 가정은 \(y=f(x)+\varepsilon \;\;(\varepsilon\text{ is noise})\)
• \(\pm \varepsilon\)정도는 맞았다고 치자
• Ridge regression과 다르게 loss가 선형적으로 증가하기 때문에 outlier에 덜 민감하게 반응하며, 노이즈에 좀 더 강건

✓ Formulation

• Estimating a linear regression

  \[f(\textbf{x})=\textbf{w}^T\textbf{x}+b\]

• with precision \(\varepsilon\) bt minimizing

✓ Primal Lagrangian

✓ \(b,w,\xi\)에 대해 미분

✓ Dual Lagrangian Problem

$$img src=’/img/Support Vector Regression(SVR) 731d2c3bb8374ee3bce20ff9a6a65397/Untitled 7.png’ width=’600’>

✓ Decision Function

✓ Dual Lagrangian Problem with Kernel Trick

✓ Decision Function

✓ Various Loss Functions for SVR

✓ C에 따른 결과 차이

C의 크기가 크면 복잡한 함수, C의 크기가 작으면 선형에 가깝다.