Published: Jan 7, 2021 by Dev-hwon
이 내용은 고려대학교 강필성 교수님의 Business Analytics 수업을 보고 정리한 것입니다.
아래 이미지 클릭 시 강의 영상 Youtube URL로 넘어갑니다.
Stochastic Neighbor Embedding
- 로컬이 아닌 거리보다 로컬 거리를 올바르게 얻는 것이 더 중요
- SNE는 쌍방향 거리가 로컬인지 여부를 결정하는 확률론적 방법을 이용한다.(but 가까운 이웃일수록 선택된 확률이 높다.)
- 각 고차원 유사성을 한 데이터 포인트가 다른 데이터 포인트를 이웃으로 선택할 확률로 변환
- Probability of picking j given in high D
- Probability of picking j given in low D
\(p_{j\mid i}\): 원래 차원(\(d\))에서 객체 \(i\)가 \(j\)를 이웃으로 선택할 확률
\(q_{j\mid i}\) : 축소된 차원(\(d'\))에서 객체 \(i\)가 \(j\)를 이웃으로 선택할 확률
p에서 가우스 반경 선택하기
- 공간의 다른 부분에서 다른 반지름을 사용하여 유효 이웃 수를 일정하게 유지
- 반경이 크면 이웃 i에 대한 분포에 대해 높은 엔트로피가 발생하는 반면, 반경이 작으면 낮은 엔트로피
- 원하는 엔트로피를 결정한 다음 해당 엔트로피를 생성하는 반경을 찾는다.
- SNE의 성능은 preplexity의 변화에 상당히 견고 (5~50)
저 차원 표현을위한 비용 함수
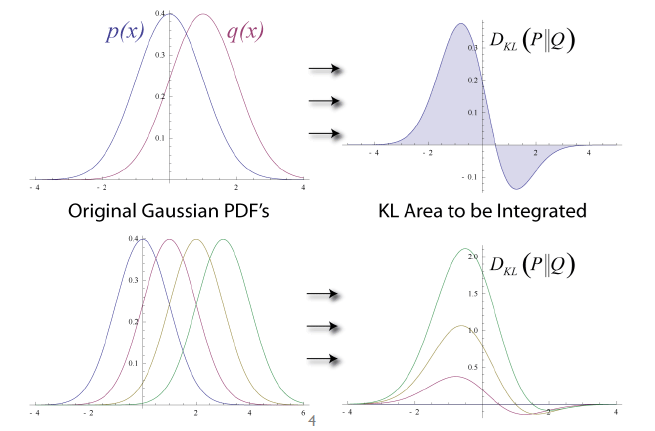
- Kullback-Leibler divergence (두 분포가 얼마나 유사한지)
- 두 확률 분포 P와 Q의 차이에 대한 비대칭 측도
0에 가까울수록 두 분포 비슷, 크면 클수록 두 분포가 다름
- Gradient
- \(\mathbf{y}_k\)는 식의 정규화 된 항을 통해 \(q_{ij}\)에 영향을 미치기 때문에 미분 비용은 장황하지만 결과는 간단하다.
- 그라디언트는 매우 단순한 형태
- Gradient of the cost function
(1) \(-\sum_ip_{t\mid i}log{q_{t\mid i}}\)을 \(\mathbf{y}_t\)에 대해서 미분한 값을 구하게 되면
\[\begin{aligned} \frac{\partial}{\partial \mathbf{y}_t}(-\sum_i p_{t|i}logq_{t|i})&=-\sum_i p_{t|i}\cdot \frac{1}{q_{t|i}}\cdot \frac{\partial q_{t|i}}{\partial \mathbf{y}_t} \\ &=-\sum_ip_{t|i}\cdot \frac{1}{q_{t|i}}\cdot \frac{d'_{it}\cdot (\sum_{k \neq i}d_{ik})-d_{it}\cdot d'_{it}}{(\sum_{k \neq i}d_{ik})^2} \\ &= -\sum_ip_{t|i}\cdot \frac{1}{q_{t|i}}\cdot \frac{-2(\mathbf{y}_t-\mathbf{y}_i)\cdot d_{it}\cdot (\sum_{k \neq i}d_{ik})+2(\mathbf{y}_t-\mathbf{y}_i)\cdot d_{it}^2)}{(\sum_{k \neq i}d_{ik})^2} \\ &=-\sum_ip_{t|i}\cdot \frac{1}{q_{t|i}}\cdot (-2(\mathbf{y}_t-\mathbf{y}_i)\cdot q_{t|i}+2(\mathbf{y}_t-\mathbf{y}_i)\cdot q_{it}^2\color{balck}) \\ &=\sum_ip_{t|i}\cdot 2(\mathbf{y}_t\color{balck}-\mathbf{y}_i\color{balck})(1-q_{t|i}) \end{aligned}\](2) \(-\sum_jp_{j\mid t}log{q_{j\mid t}}\)을 \(\mathbf{y}_t\)에 대해서 미분한 값을 구하게 되면
\[\begin{aligned} \frac{\partial}{\partial \mathbf{y}_t}(-\sum_j p_{j|t}logq_{j|t})&=-\sum_j p_{j|t}\cdot \frac{1}{q_{j|t}}\cdot \frac{\partial q_{j|t}}{\partial \mathbf{y}_t} \\ &=-\sum_jp_{j|t}\cdot \frac{1}{q_{j|t}}\cdot \frac{d'_{tj}\cdot (\sum_{k \neq t}d_{tk})-d_{tj}\cdot (\sum_{k \neq t}d'_{tk})}{(\sum_{k \neq t}d_{tk})^2} \\ &= -\sum_jp_{j|t}\cdot \frac{1}{q_{j|t}}\cdot \frac{-2(\mathbf{y}_t-\mathbf{y}_j)\cdot d_{tj}\cdot (\sum_{k \neq t}d_{tk})-d_{tj}\cdot (\sum_{k \neq t}d'_{tk})}{(\sum_{k \neq t}d_{tk})^2} \\ &=2\sum_jp_{j|t}\cdot (\mathbf{y}_t-\mathbf{y}_j)+\sum_j p_{j|t}\cdot \frac{\sum_{k \neq t}d'_{tk}}{\sum_{k \neq t}d_{tk}} \\ &=2\sum_jp_{j|t}\cdot (\mathbf{y}_t\color{balck}-\mathbf{y}_j\color{balck})+\sum_j \cdot \frac{d'_{tj}}{\sum_{k \neq t}d_{tk}}\\ &=2\sum_jp_{j|t}\cdot (\mathbf{y}_t\color{balck}-\mathbf{y}_j\color{balck})-2\sum_{j}(\mathbf{y}_t-\mathbf{y}_j)\cdot \frac{d_{tj}}{\sum_{k \neq t}d_{tk}}\\ &=2\sum_jp_{j|t}\cdot (\mathbf{y}_t\color{balck}-\mathbf{y}_j\color{balck})-2\sum_{j}(\mathbf{y}_t-\mathbf{y}_j)\cdot q_{j|t}\\ &=2\sum_j (\mathbf{y}_t-\mathbf{y}_j)(p_{j|t}-q_{j|t})\end{aligned}\](3) \(-\sum_{i \neq t}\sum_{j \neq t}p_{i\mid j}log{q_{i\mid j}}\)을 \(\mathbf{y}_t\)에 대해서 미분한 값을 구하게 되면
\[\begin{aligned} \frac{\partial}{\partial \mathbf{y}_t}(-\sum_{i \neq t}\sum_{j \neq t} p_{i|j}logq_{i|j})&=-\sum_{i \neq t}\sum_{j \neq t} p_{i|j}\cdot \frac{1}{q_{i|j}}\cdot \frac{\partial q_{i|j}}{\partial \mathbf{y}_t} \\ &=-\sum_{i \neq t}\sum_{j \neq t}p_{i|j}\cdot \frac{1}{q_{i|j}}\cdot \frac{d'_{ji}\cdot \sum_{k \neq j}d_{jk}-d_{ji}\cdot d'_{jt}}{(\sum_{k \neq j}d_{jk})^2} \\ &= -\sum_{i \neq t}\sum_{j \neq t}p_{i|j}\cdot \frac{1}{q_{i|j}}\cdot \frac{2(\mathbf{y}_t-\mathbf{y}_j)\cdot d_{ji}\cdot d_{jt}}{(\sum_{k \neq j}d_{jk})^2} \\ &=-\sum_{i \neq t}\sum_{j \neq t}p_{i|j}\cdot \frac{1}{q_{i|j}}\cdot 2(\mathbf{y}_t-\mathbf{y}_j)\cdot q_{i|j}\cdot q_{t|j} \\ &=-\sum_{i \neq t}\sum_{j \neq t}2(\mathbf{y}_t-\mathbf{y}_j)\cdot p_{i|j}\cdot q_{t|j} \end{aligned}\](1)과 (3)을 더하면
\[\sum_ip_{t|i}\cdot 2(\mathbf{y}_t\color{balck}-\mathbf{y}_i\color{balck})(1-q_{t|i})-\sum_{i \neq t}\sum_{j \neq t}2(\mathbf{y}_t-\mathbf{y}_j)\cdot p_{i|j}\cdot q_{t|j}\]| 여기서 앞에 $$\sum_ip_{t | i}\cdot 2(\mathbf{y}t\color{balck}-\mathbf{y}_i\color{balck})(1-q{t | i})$$에서 i는 j로 치환될 수 있다. |
(1) + (3) 구한 값에 (2)를 더하면
\[\begin{aligned} 2\sum_j(\mathbf{y}_t-\mathbf{y}_j)(p_{t|j}-q_{t|j})+2\sum_j (\mathbf{y}_t-\mathbf{y}_j)(p_{j|t}-q_{j|t}) \\ =2\sum_j(\mathbf{y}_t-\mathbf{y}_j)(p_{t|j}-q_{t|j}+p_{j|t}-q_{j|t}) \end{aligned}\]- 비용 함수를 최소화하기 위해 더 낮은 차원의 좌표를 업데이트
- Gradient update with a momentum term
- 조건부 확률을 쌍별 확률로 바꾸기
- cost frunction and gradient
- Crowding problem
- 비교적 먼 데이터 포인트를 수용하는 영역이 근처 데이터 포인트를 수용하는 영역에 비해 충분히 크지 않다.
t-SNE
Resolution to the Crowding problem
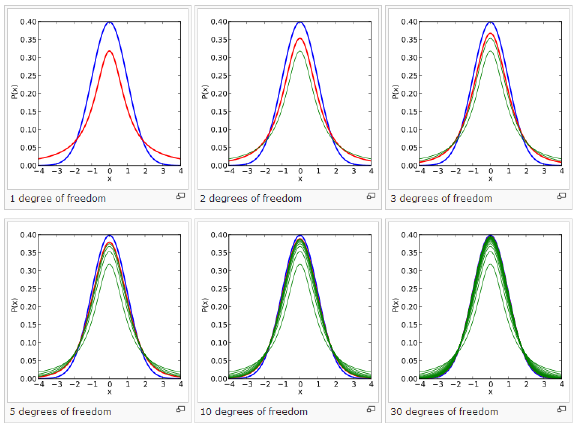
- 가우시안보다 꼬리가 두터운 확률 분포를 사용하여 저차원지도에서 거리를 확률로 변환
- 자유도가 1 인 Student’s t 분포
Optimization of t-SNE
\[p_{ij}=\frac{e^{-\frac{\|\mathbf{X}_i-\mathbf{X}_j\|^2}{2\sigma^2_i}}}{\sum_{k \neq l}e^{-\frac{\|\mathbf{X}_k-\mathbf{X}_l\|^2}{2\sigma^2_i}}} \;\;\;\;\; q_{j|i}=\frac{(1+\|\mathbf{y}_i-\mathbf{y}_j\|^2)^{-1}}{\sum_{k \neq l}(1+\|\mathbf{y}_k-\mathbf{y}_l\|^2)^{-1}}\]- Gradient:
t-SNE algorithm

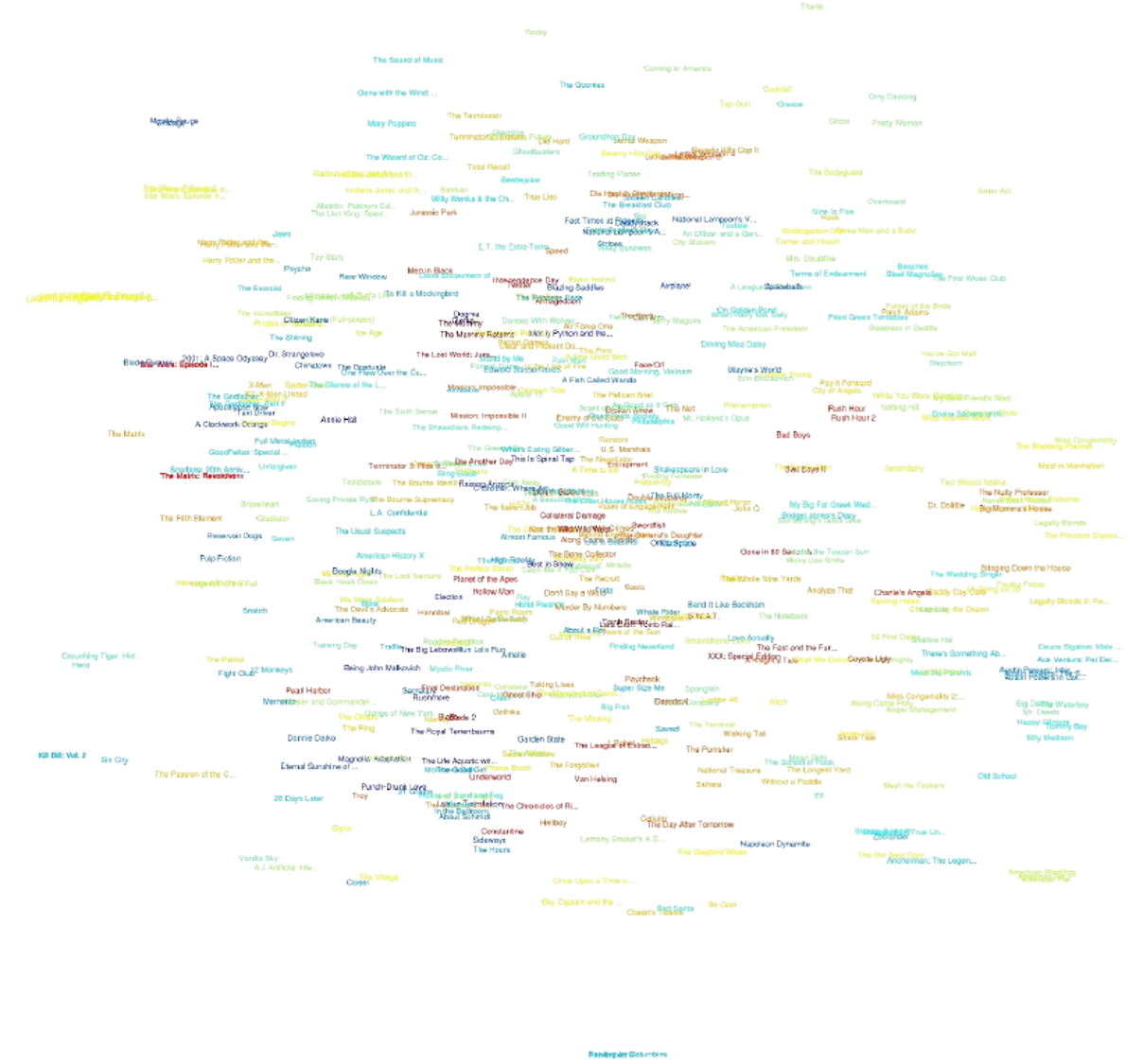
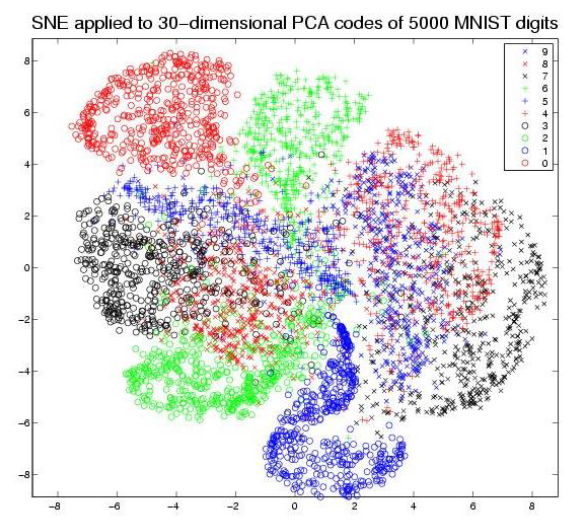
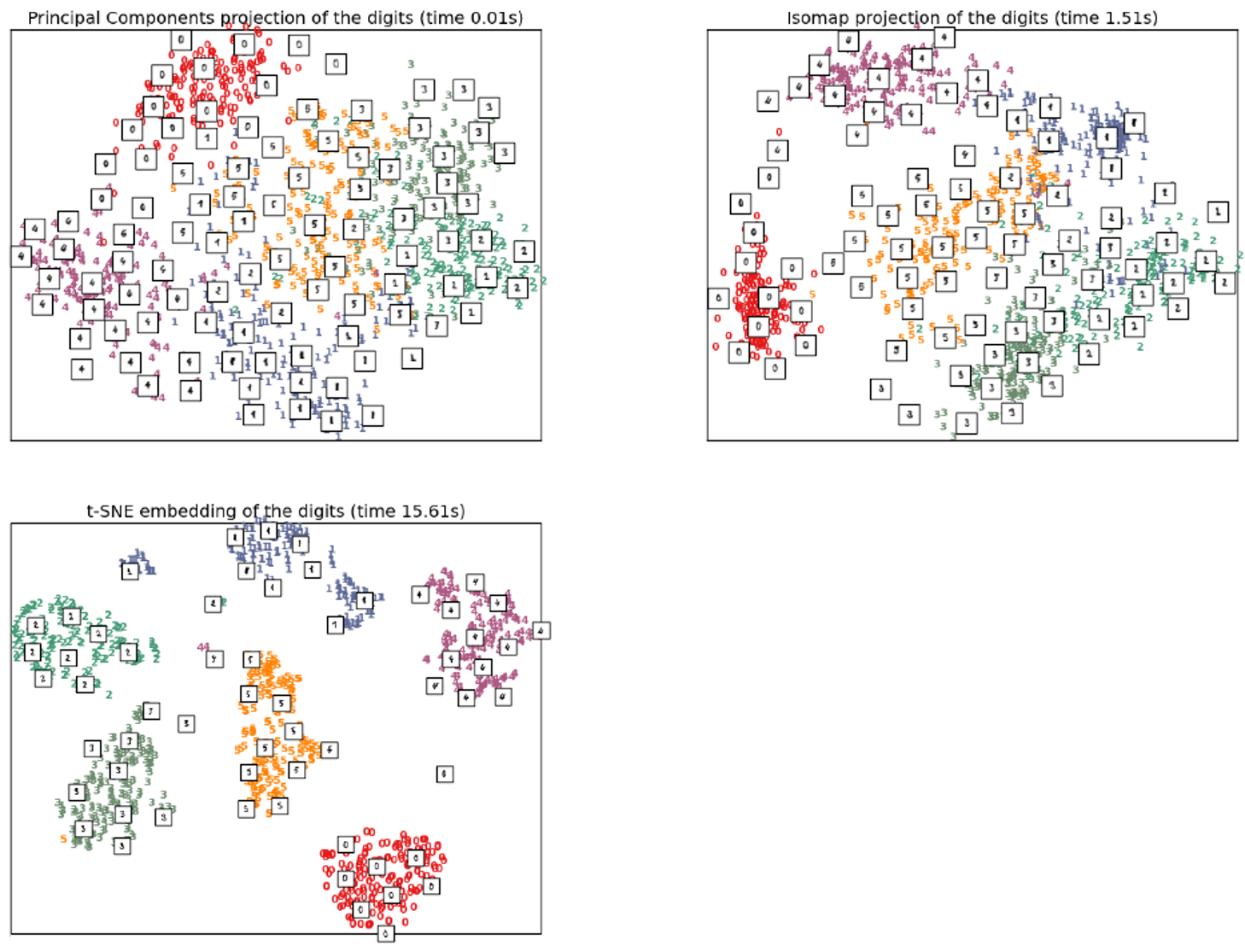
t-SNE Example
- Mnist dataset


- Olivetti faces datasets

- Netflix dataset