Published: Jan 1, 2021 by Dev-hwon

이 내용은 고려대학교 강필성 교수님의 Business Analytics 수업을 보고 정리한 것입니다.

아래 이미지 클릭 시 강의 영상 Youtube URL로 넘어갑니다.

Isometric Feature Mapping (Isomap)

• PCA와 MDS의 주요 알고리즘 기능을 결합
  • 계산 효율성, 글로벌 최적 성 및 점근 적 수렴 보장
• MDS와 Distance metrics 변환하는 부분만 다르다.
• 클래식 MDS를 기반으로 구축되지만 모든 데이터 쌍 사이의 지오데식 매니폴드 거리에 포착된 데이터의 고유 형상을 보존하고자 함.

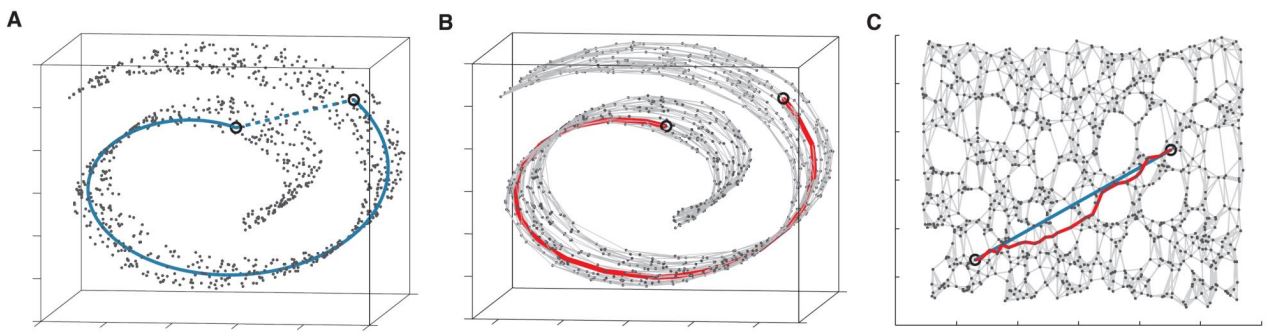
Isomap procedure

• Step 1: Construct neighborhood graph
  • \(\varepsilon\)-Isomap: 반경 \(\varepsilon\) 안에 있는 모든 이웃들을 엣지로 연결
  • \(k\)-Isomap: 거리가 아닌 특정한 객체를 기준으로 k개 이웃을 이어주는 방법
• Step 2: Compute the shortest paths
  • \(i\)와 \(j\)가 엣지로 연결되어 있으면 \(d_G(i,j)=d_X(i,j)\)로 초기화하고 아니면 \(d_G(i,j)=\text{inf}\)
  • 𝑘 = 1,2,…, N의 각 값에 대해 모든 항목 \(d_G(i,j)\)를 \(min \{d_G(i,j), d_G(i,k) + d_G(k,i)\)로 바꾼다.
• Step 3: Construct d-dimensional embedding by traditional MDS

Example

• Hand digit recognition

---

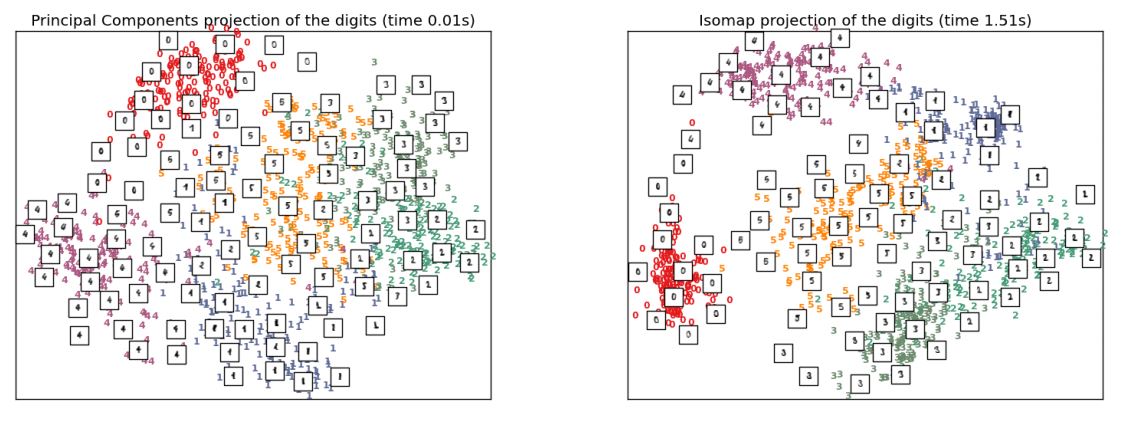
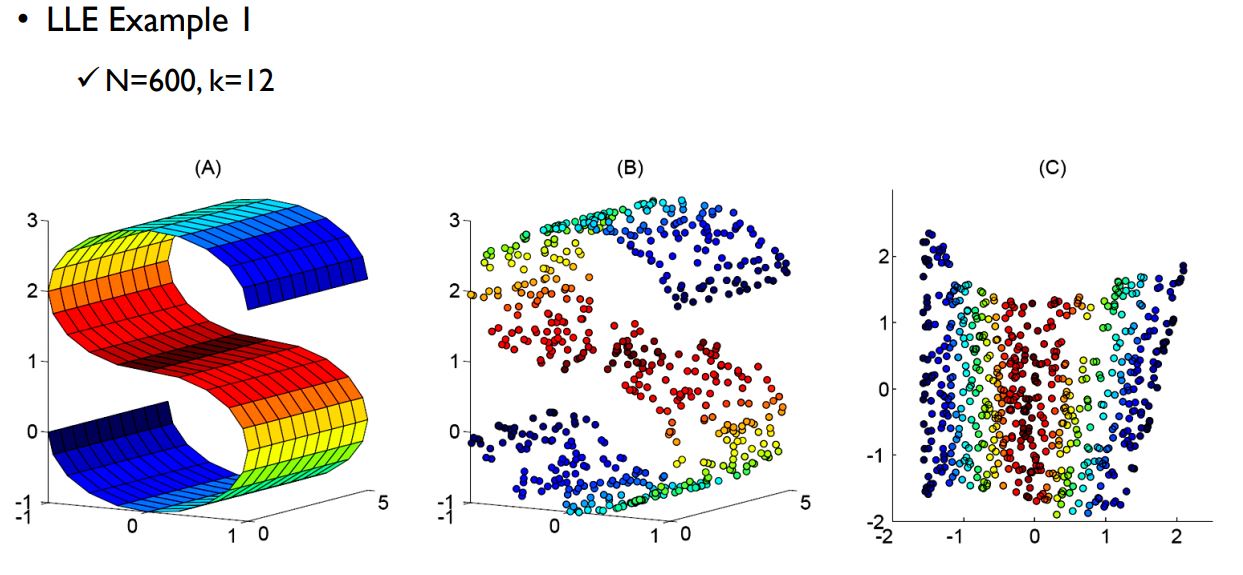
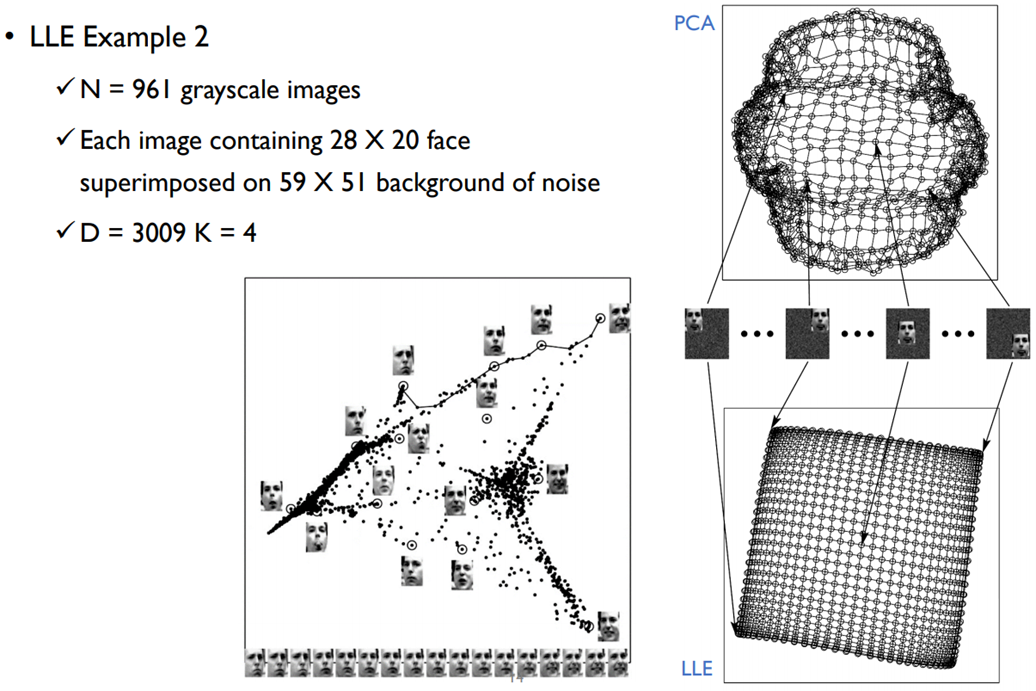
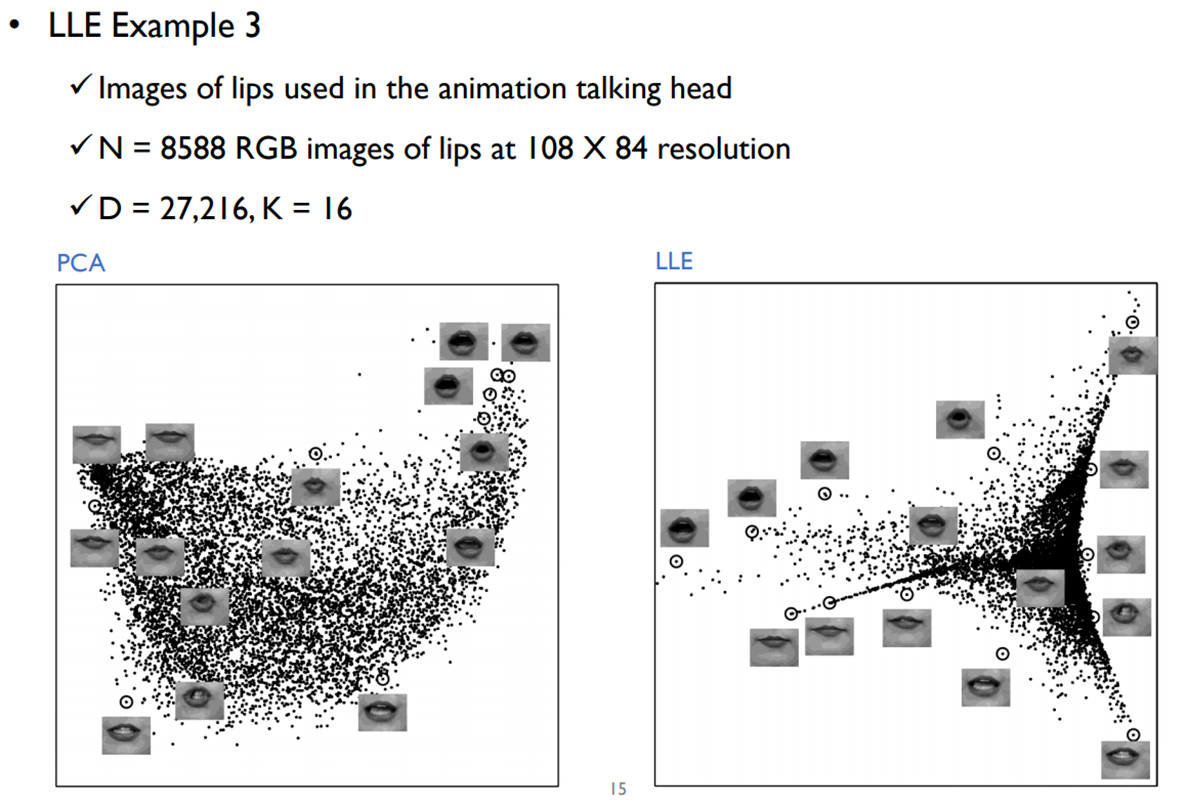
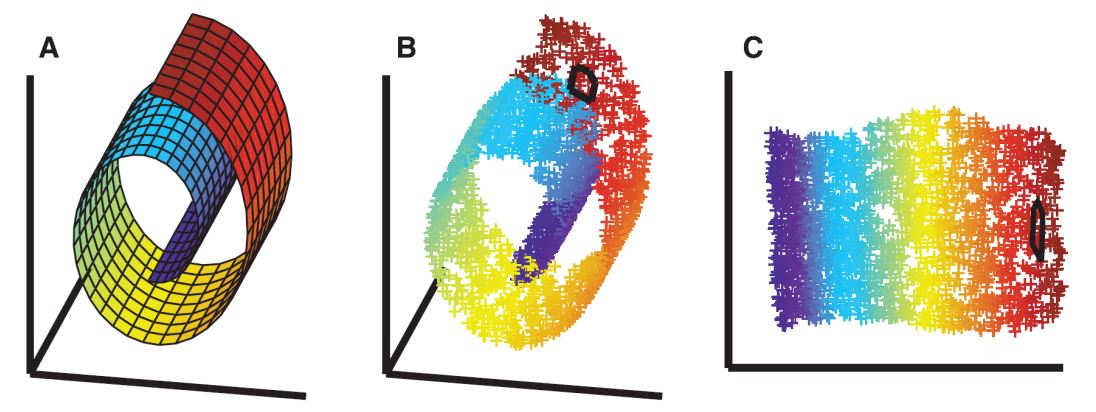
Locally Linear Embedding (LLE)

• 비선형 차원 감소를 위한 고유 벡터 방법
  • 간단한 구현
  • local minima에 빠지지 않는다.
  • 높은 비선형 임베딩 생성 가능
  • 고차원 데이터를 더 낮은 차원의 단일 글로벌 좌표계로 매핑

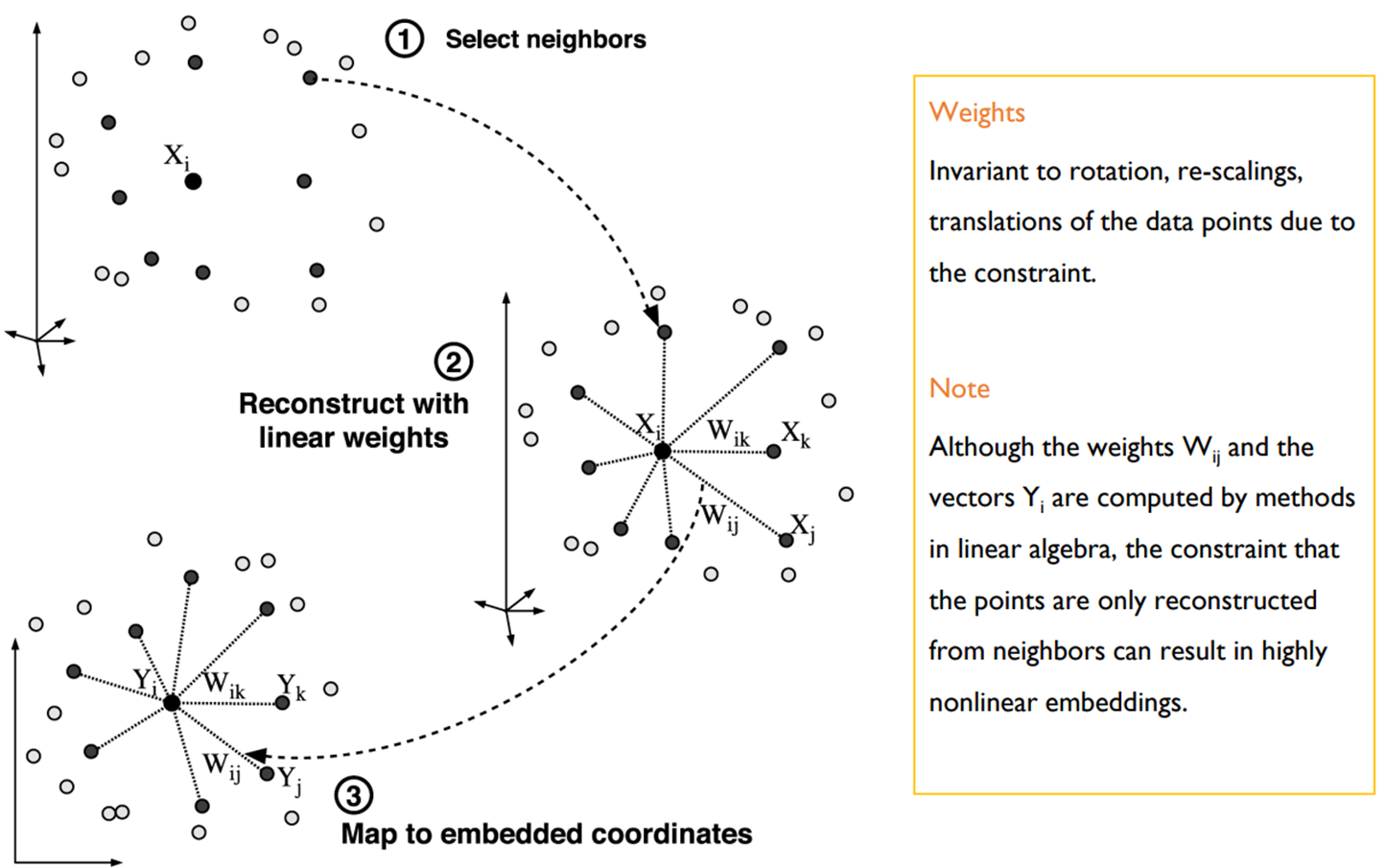
LLE procedure

• Step 1: 각 데이터 포인트의 이웃 계산

• Step 2: 인접 선형 피팅을 통해 비용 함수를 최소화하면서 각 데이터 포인트를 이웃으로부터 가장 잘 재구성하는 가중치 \(W_{ij}\)를 계산 (자신을 최적으로 재구축 할 수 있는 이웃들의 가중치 찾기)

\[E(\mathbf{W})=\sum_i|\mathbf{x}_i-\sum_j\mathbf{W}_{ij}\mathbf{x}_j|^2\] \[s.t. \mathbf{W}_{ij}=0 \text{ if }\mathbf{x}_j\text{ does not belong to the neighbor of }\mathbf{x}_i\] \[\sum_j\mathbf{W}_{ij}=1 \text{ for all }i\]

\(\mathbf{X}\)를 알고 있으므로 \(\mathbf{W}\)를 최적화

• Step 3: 가중치 \(\mathbf{W}_{ij}\)로 가장 잘 재구성 된 벡터를 계산하여 아래쪽이 0이 아닌 고유 벡터로 2 차 형태를 최소화

\[\Phi(\mathbf{W})=\sum_i|\mathbf{y}_i-\sum_j\mathbf{W}_{ij}\mathbf{y}_j|^2\]

이번엔 \(\mathbf{W}\)를 알고 있으므로 \(\mathbf{Y}\)를 최적화

이해를 위해 계산되는 공식을 이미지로 대체 합니다.

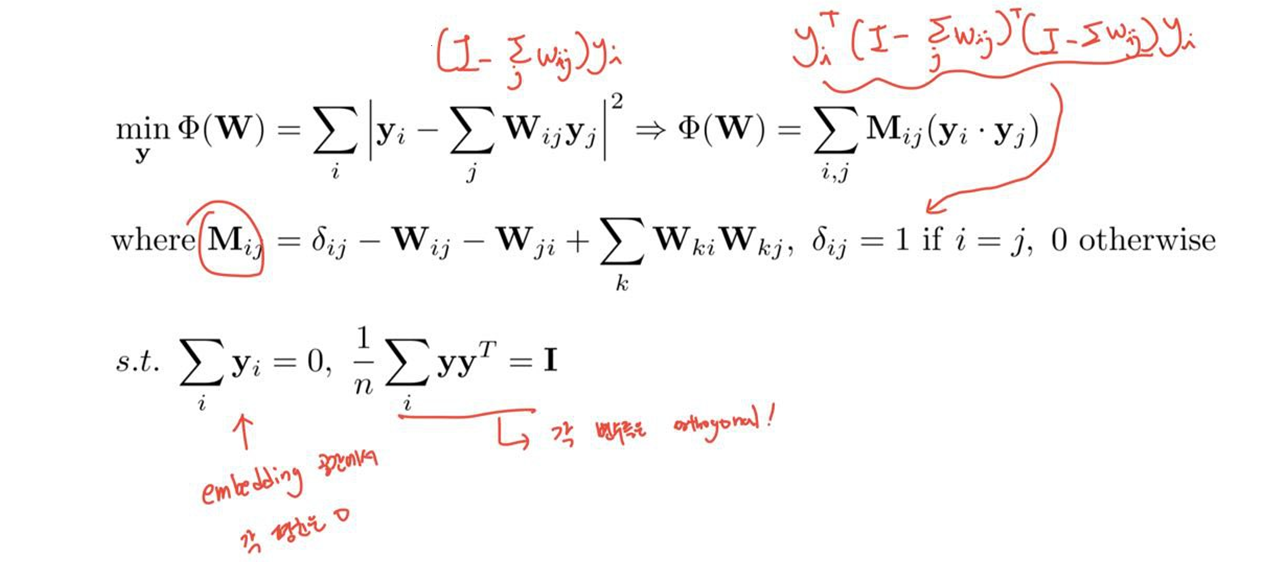
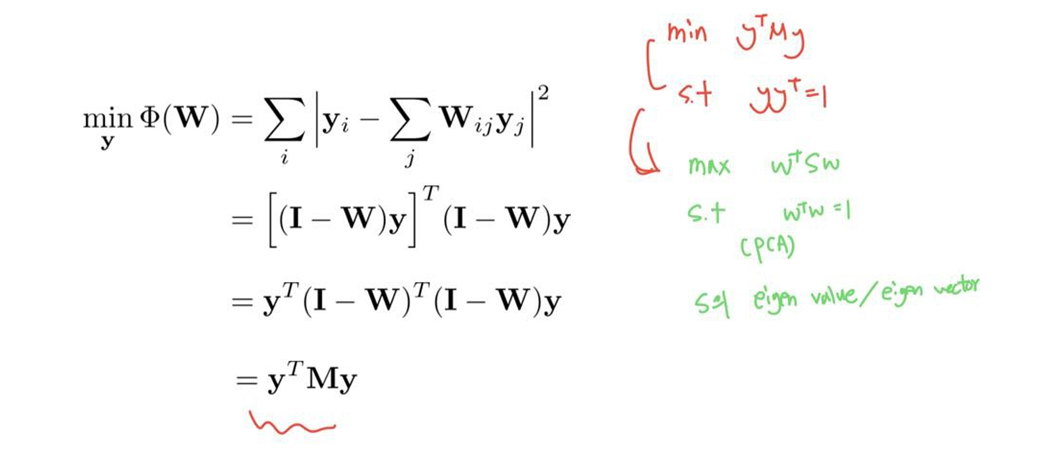
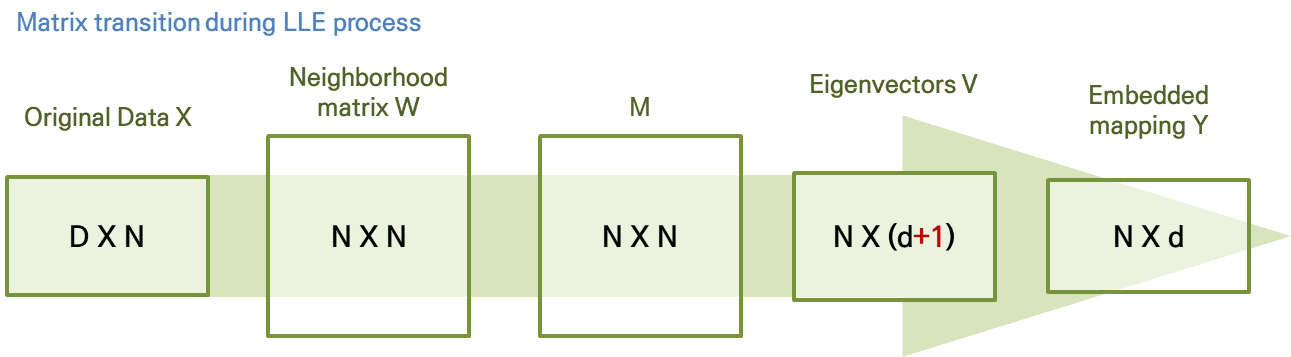
• 최적의 임베딩은 행렬 M (Rayleitz-Ritz 정리)의 하위 d + 1 고유 벡터를 계산하여 구한다.
• 하단 고유 벡터는 모든 구성 요소가 동일한 단위 벡터입니다.
• 이 고유 벡터를 버리면 임베딩의 평균이 0이라는 제약 조건이 적용된다.

---

Example