Published: Dec 29, 2020 by Dev-hwon
이 내용은 고려대학교 강필성 교수님의 Business Analytics 수업을 보고 정리한 것입니다.
아래 이미지 클릭 시 강의 영상 Youtube URL로 넘어갑니다.
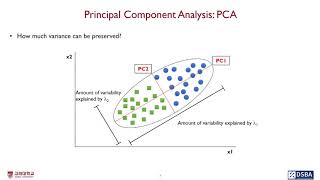
Principal Component Analysis: PCA
- 원데이터의 분산을 최대한 보존하는 직교하는 기저를 찾는것
- 데이터가 가지고 있는 특정한 속성을 최대한 보존하는 방향으로 새로운 성분을 만들어내는 것
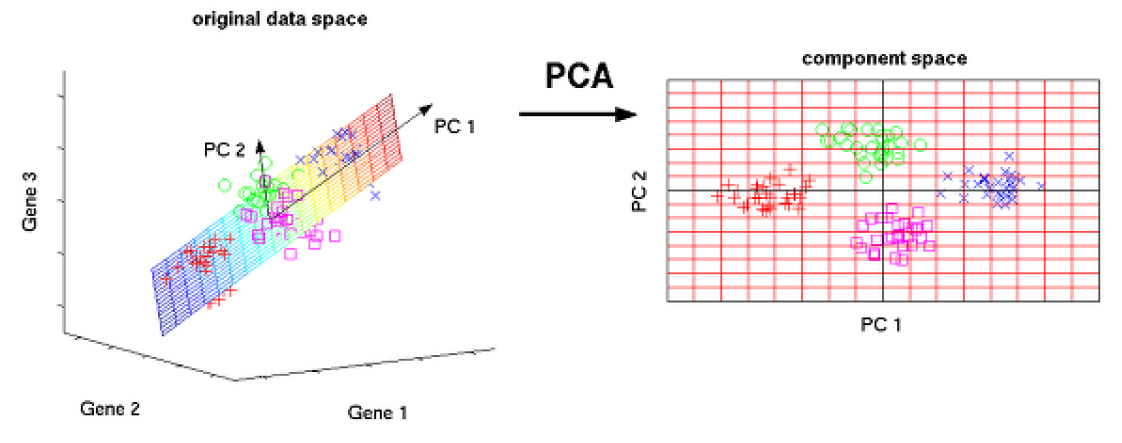
목적
- 기준에 따라 예측 후 최대한 분산을 보존 할 수있는 기준 집합을 찾는다.
- \(X_1, X_2, \cdots, X_p\): Original variables
- \(\mathbf{a}_i=[a_{i1}, a_{i2}, \cdots, a_{ip}]\): \(i^{th}\) basis or principal component
- \(Y_1, Y_2, \cdots, Y_p\): variables after the projection onto the \(i^{th}\) basis
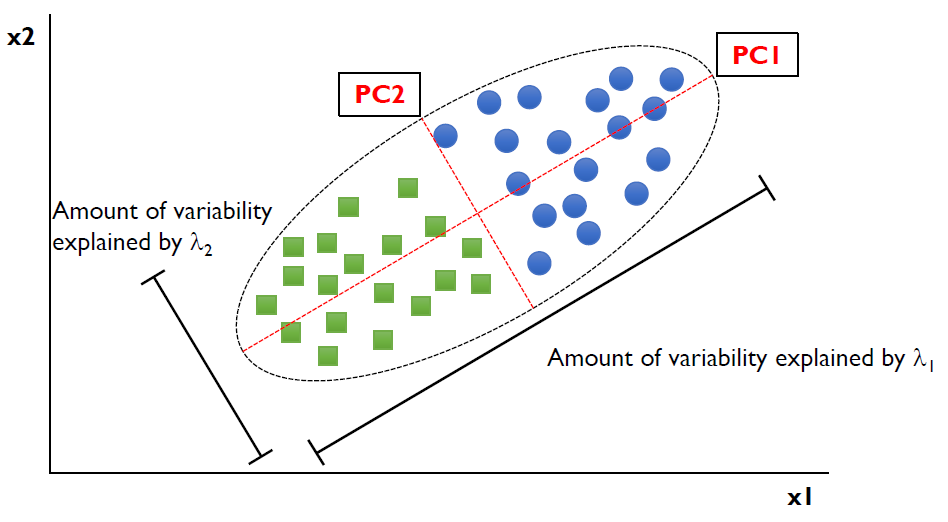
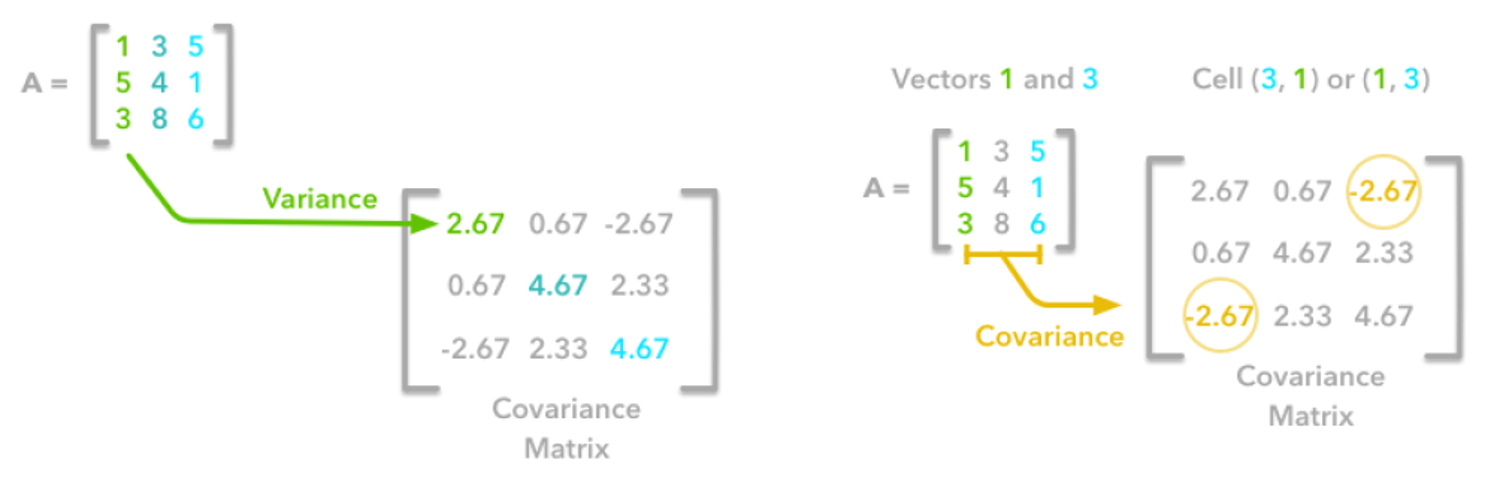
Covariance
- \(\mathbf{X}\): a data set (d by n, d: # of variables, n: # of records, 여기서 벡터는 column-wise vector)
- \[Cov(\mathbf{X})_{ij}=Cov(\mathbf{X})_{ji}\]
- Total variance of the data set: \(tr[Cov(\mathbf{X})]=Cov(\mathbf{X})_{11}+Cov(\mathbf{X})_{22}+\cdots+Cov(\mathbf{X})_{dd}\)
Projection onto a basis

\(p\)는 사영 후 값, \(\vec{b}\)는 \(x\)는 pc
Eigenvalue와 Eigenvector
- 행렬 A가 주어지면 다음 방정식을 만족하는 스칼라 값 𝜆과 벡터 x를 각각 Eigenvalue(고유 값)과 Eigenvector(고유 벡터)라고 한다.
- 행렬을 벡터에 곱하면 선형 변환이 수행된다.
- 고유 벡터는 변환에 의해 방향을 변경하지 않는다.
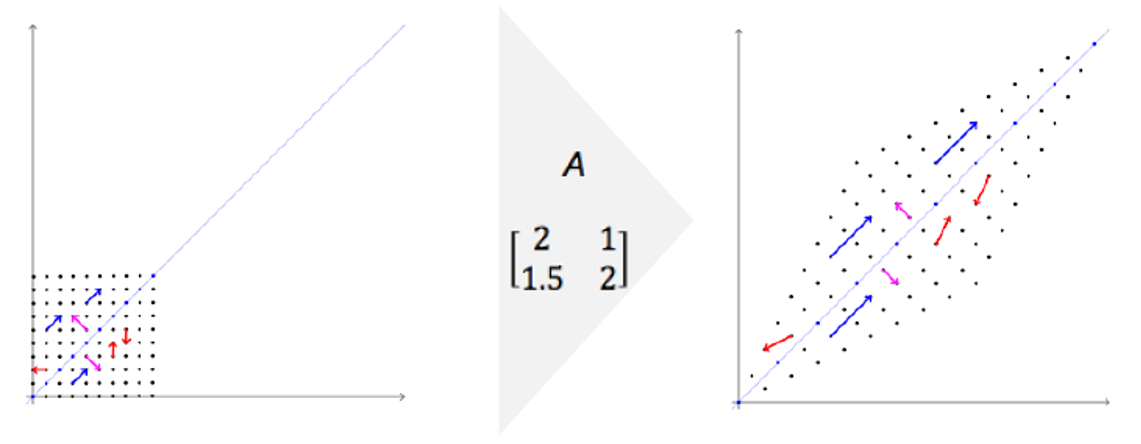
- 크기만 바뀌고 방향이 바뀌지 않는 벡터 -> Eigenvector
- 크기가 바뀐경우 변화된 양 -> Eigenvalue
- 행렬 A가 non-singular d x d 행렬인 경우(역행렬이 존재)
- d 개의 Eigenvalue-Eigenvector 쌍이 있다.
- Eigenvector(고유 벡터)는 서로 직교
Step 1: Data Centering
- 변수의 평균을 0으로 만든다.
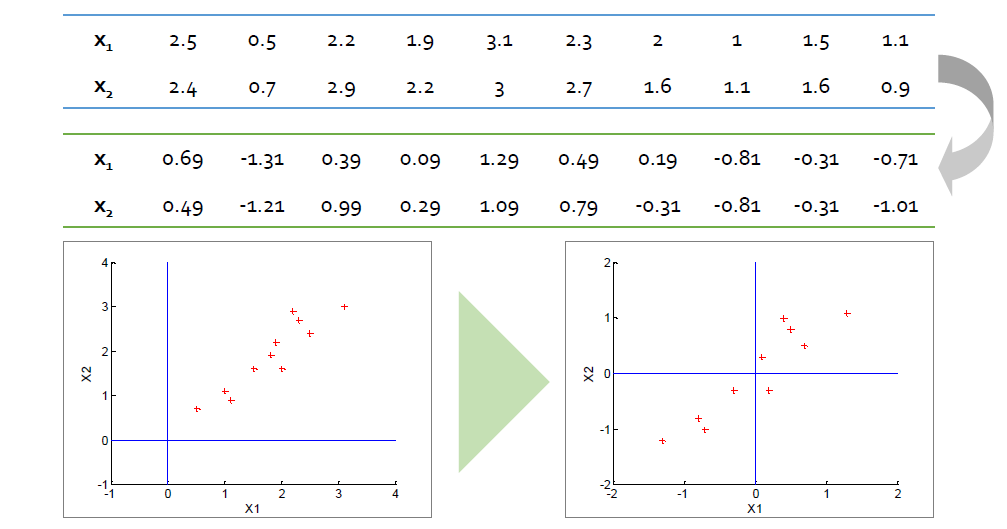
Step 2: Formulate the optimization problem
- 벡터 x가 기저 w에 투영 후 분산
-
\(\mathbf{S}\)는 \(\mathbf{x}\)가 정규화되는 표본 공분산 행렬
-
PCA의 목적은 투영 후 분산 V를 최대화하는 것
Step 3: Obtain the solution
- 라그랑주 승수법(Lagrangian multiple)을 사용하면
Step 4: Find the base set of bases
- 고유 값의 내림차순으로 고유 벡터 정렬
- \(\mathbf{w}_1\)을 고유 벡터 중 하나이고 \(\lambda_1\)을 해당 고유 값으로 지정한다.
- 𝐰1에 투영 된 샘플의 변형은
- 이 예에서 하나의 기준으로 원래 분산의 96%를 보존 할 수 있다.
Step 5: Extract new features
- 선택한 베이스에 원본 데이터를 투영
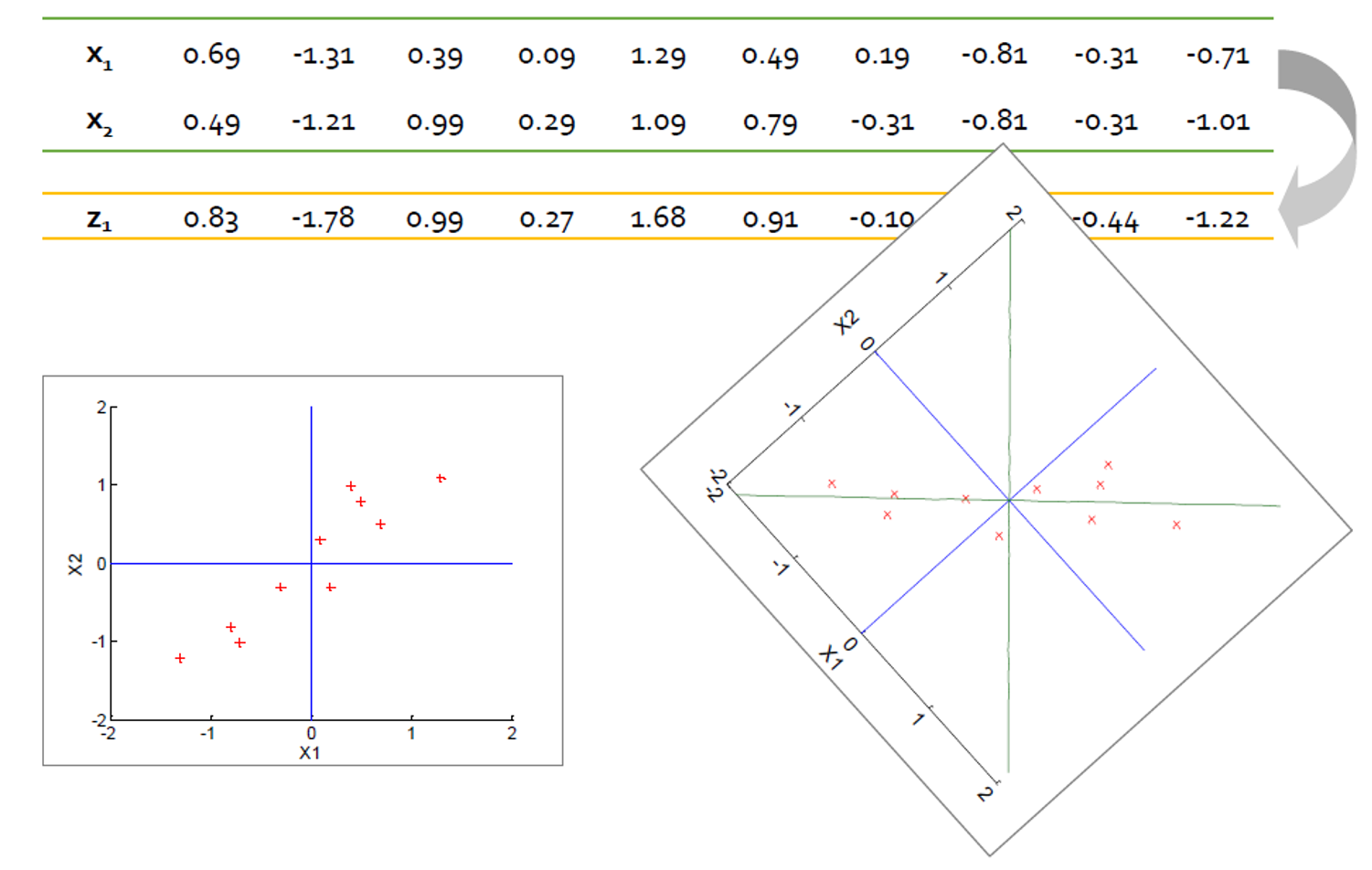
Step 6: Reconstruct the original data
- 투영된 공간의 데이터를 원래 공간으로 재구성이 가능하다.
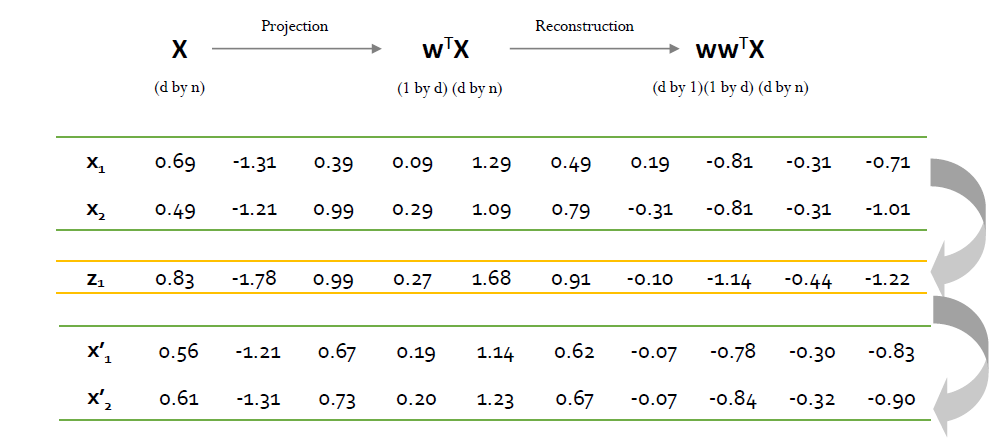
최적의 주성분은 몇 개인가?
- 명시적인 해결책 없음
- 분산 보존률 및 도메인 전문가의 지식을 바탕으로 결정 가능
- 공분산, 고유값 고유벡터의 속성에 따라
- 데이터 세트의 총 변수 = 표본 공분산 행렬의 고유 값 합계
- k 번째 기준에 데이터를 투영하면 보존되는 분산의 양은 다음과 같다.
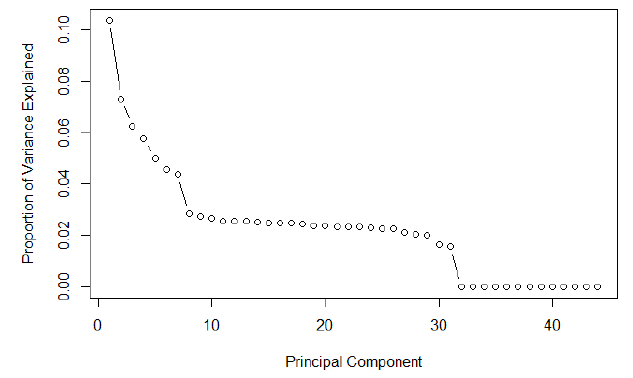
- Scree 플롯은 일반적으로 PC 수를 결정하는 데 사용된다.
- x 축 : PC 색인
- y 축 : 해당 고유 값
- Scree 플롯은 초기 단계에서 빠르게 감소한다.
- 일부 포인트 이상으로 감소하지 않는다.
- 선택 방법 1 : 엘보 포인트 찾기
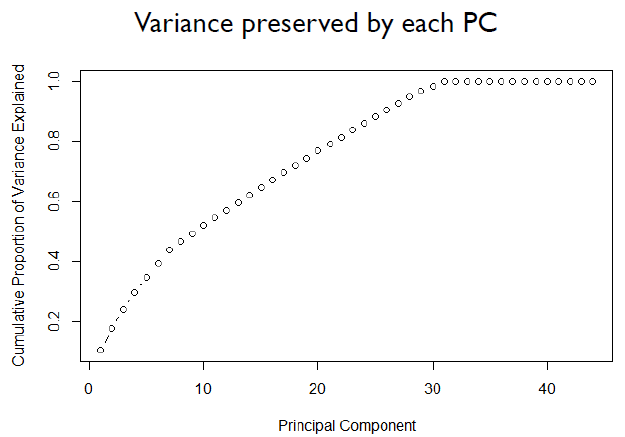
- 선택 방법 2 : 미리 결정된 필수 분산(80%)을 유지하는 가장 작은 PC 찾기
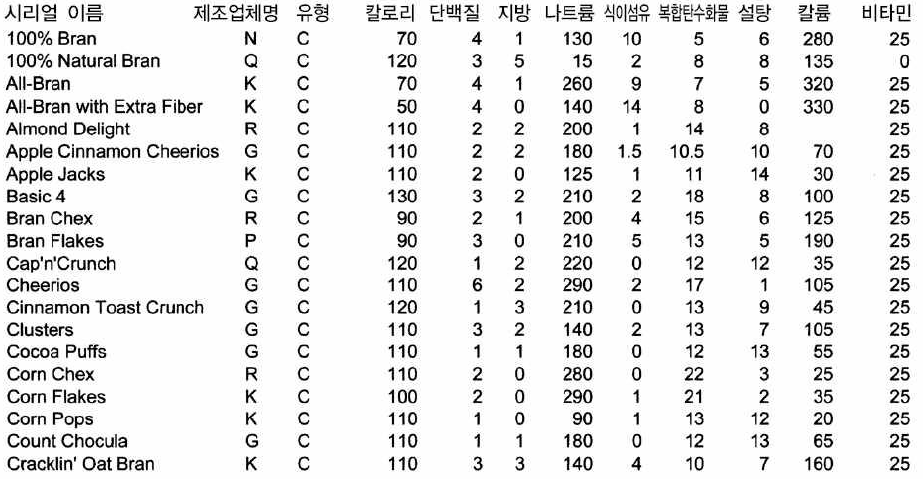
PCA 예제
- 원 데이터
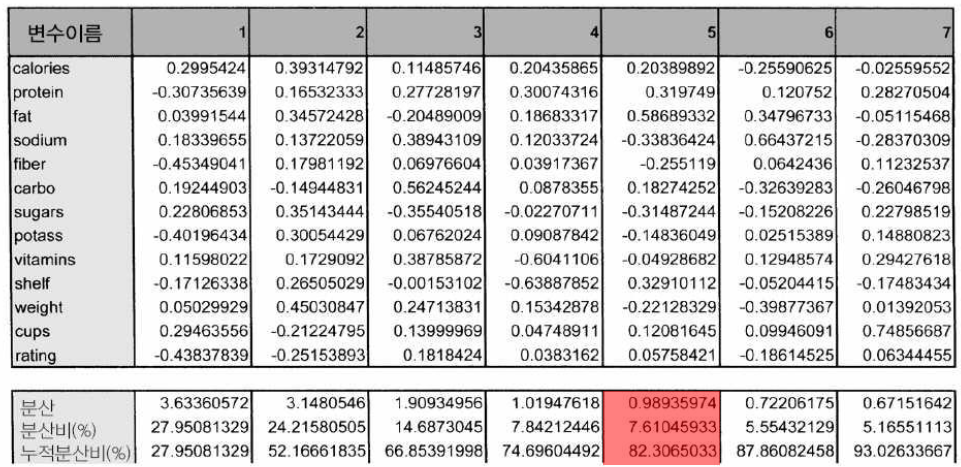
- 각 주성분에 대한 고유 벡터 고유 값
- 전체 분산의 80 % 이상을 유지하려면 최소 5 PC가 필요하다.
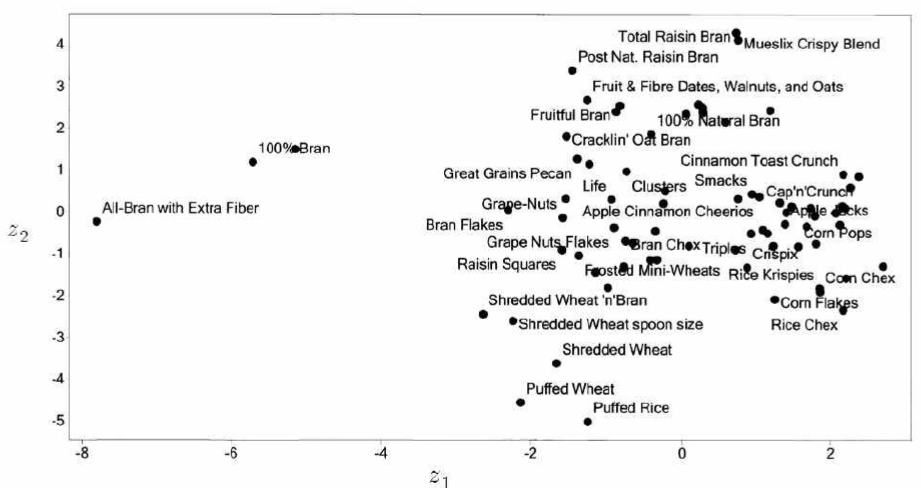
- 2차원으로 나타낸 결과
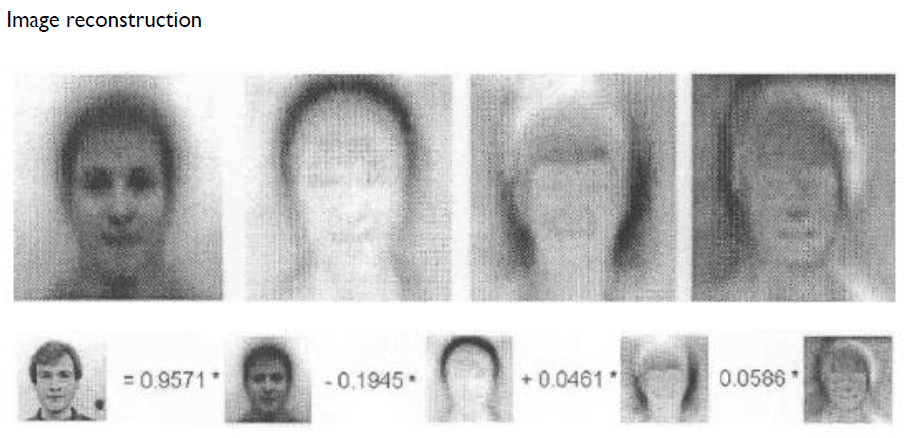
- 얼굴 이미지 데이터

PCA 한계
- non-Gaussian 또는 multimodal Gaussian 분포에서는 잘 작동하지 않는다.

- 분류와는 적합하지 않다.
- 분류에는 (F)LDA / Linear Discriminant Analysis 방법이 있음
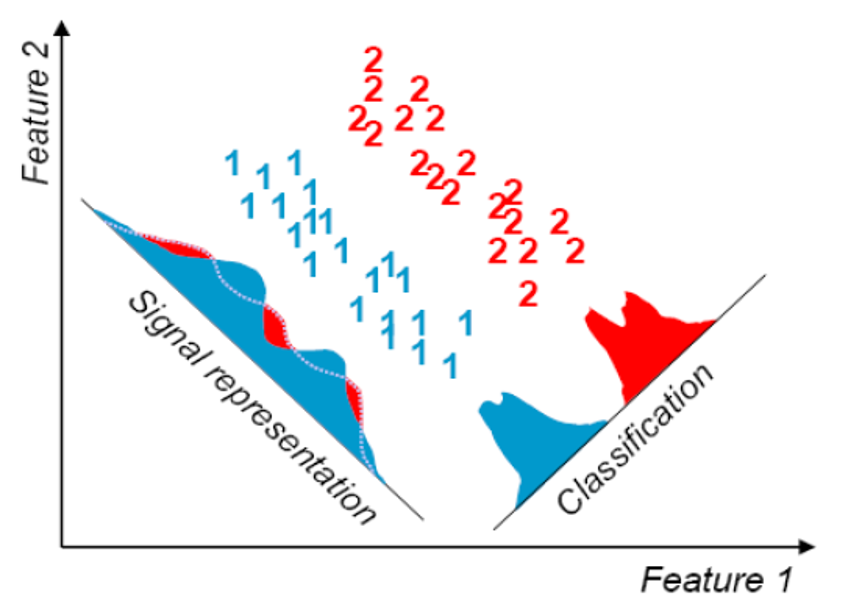
- 분류에는 (F)LDA / Linear Discriminant Analysis 방법이 있음