연관 규칙 분석

Published: Jun 16, 2020 by Dev-hwon

연관 규칙 분석(Association Rule Analysis)

서로 다른 두 아이텝 집합이 얼마나 빈번히 발생하는지 연관도를 알 수 있다.

1. 빈번 아이템 집합

같은 트랜잭션에서 같이 발생할 확률이 높은 아이템

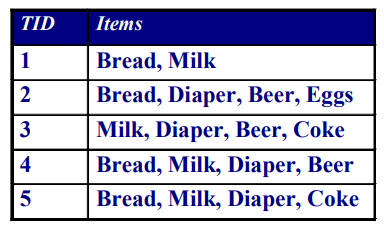
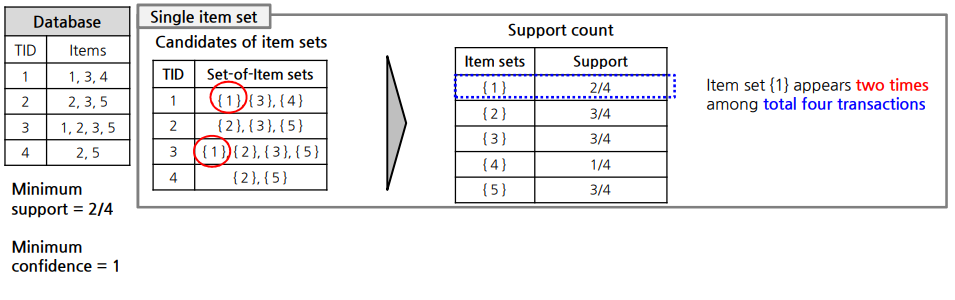
1) Item set

하나 이상의 아이템 집합(예: {Milk, Bread, Diaper})
k-item set: k개의 아이템을 포함하는 item set

2) Support count($\sigma$)

item set의 발생 빈도(예: $\sigma$({Milk, Bread, Diaper})=2)

3) Support

item set가 포함된 transaction 비율(예: s({Milk, Bread, Diaper})=2/5)

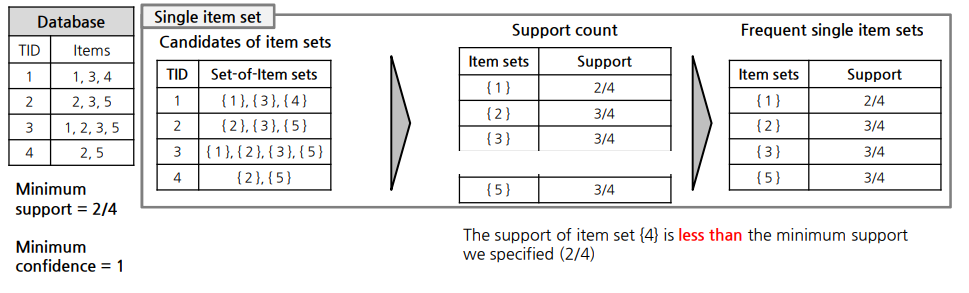
4) Frequent item set

support count가 minsup(minimum support count) 임계값보다 크거나 같은 항목 세트

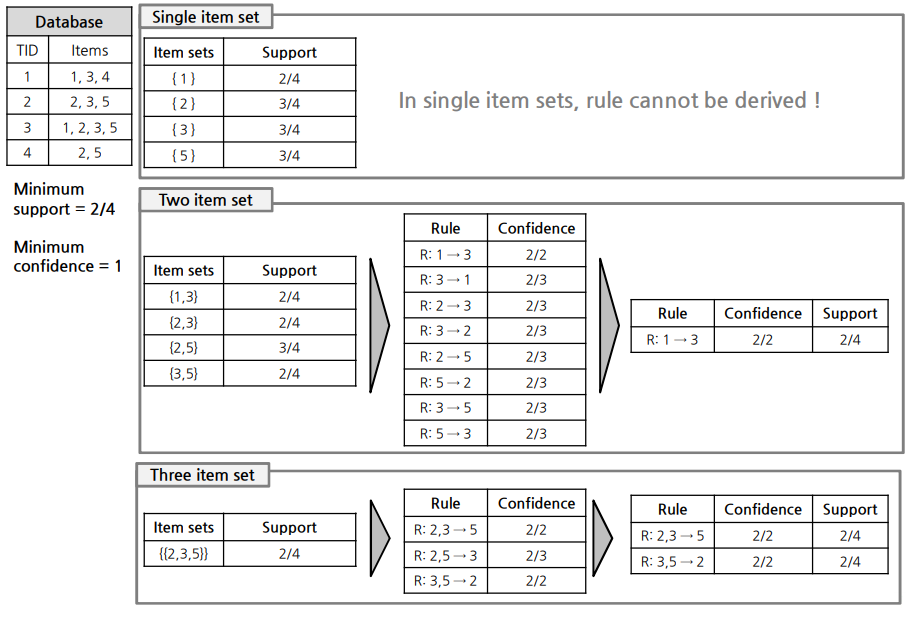
2. 연관 규칙

$X \rightarrow Y$ 형식의 의미 표현 (예: {Milk, Diaper}$\rightarrow${Beer})
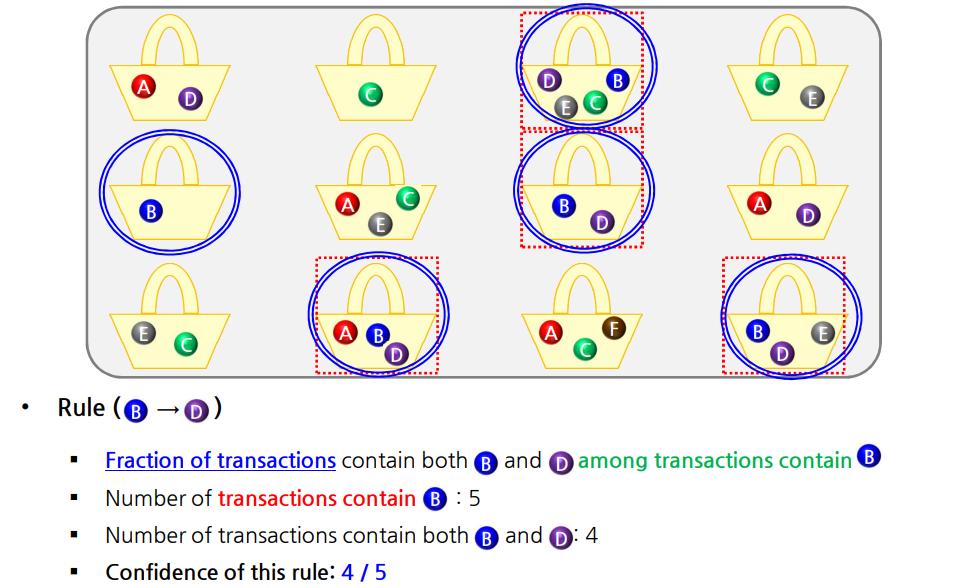
Rule evaluation metrics

Support(s): X와 Y를 모두 포함한다는 거래의 비율 ($P(X\cap Y)$)

Confidence(c): X가 포함된 트랜잭션에서 Y의 아이템이 얼마나 자주 나타나는지 측정($$P(X \cap Y)/P(X)=P(Y

X)$$)

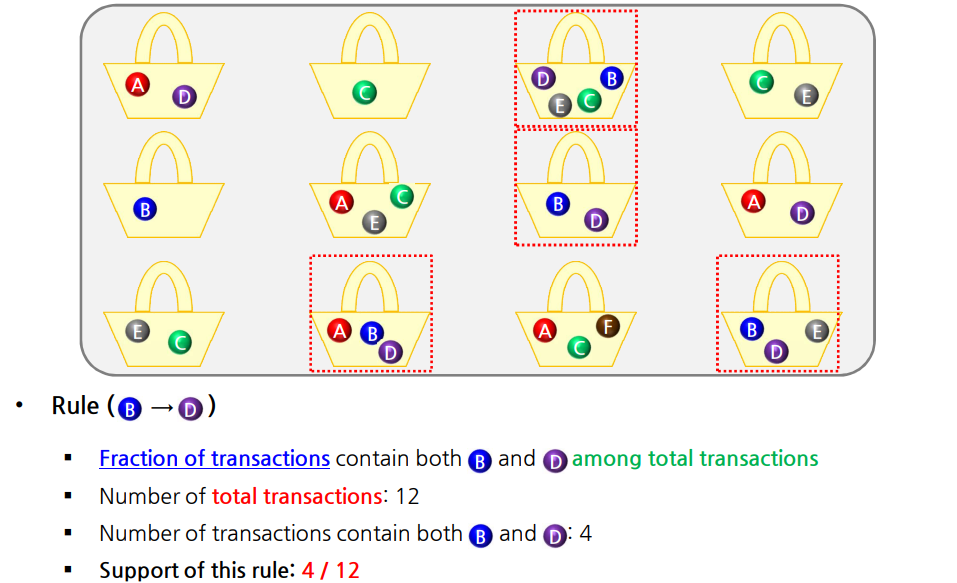
3. 무차별 접근 방식

1) 가능한 모든 연관 규칙 나열

2) 각 규칙에 대한 support, confidence 계산

3) 최소 support, confidence 임계값을 넘지 않는 규칙 제거

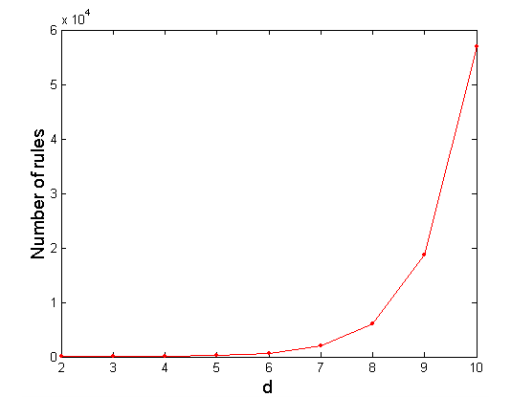
계산 복잡도: 총 아이템수 $d \rightarrow$ 총 아이템 세트수 $2^d$

4. 2단계 접근 방식

1) 빈번 아이템 세트 생성: support가 최소 support 이상인 모든 항목 세트 생성

2) 규칙 생성: 각 규칙이 빈번 아이템 세트의 이진 파티셔닝인 각 빈번 아이템 세트에서 confidence가 높은 규칙 생성

빈번 아이템 세트의 생성은 여전히 계산 비용이 많이 든다

5. 후보자 수를 줄이는 방법

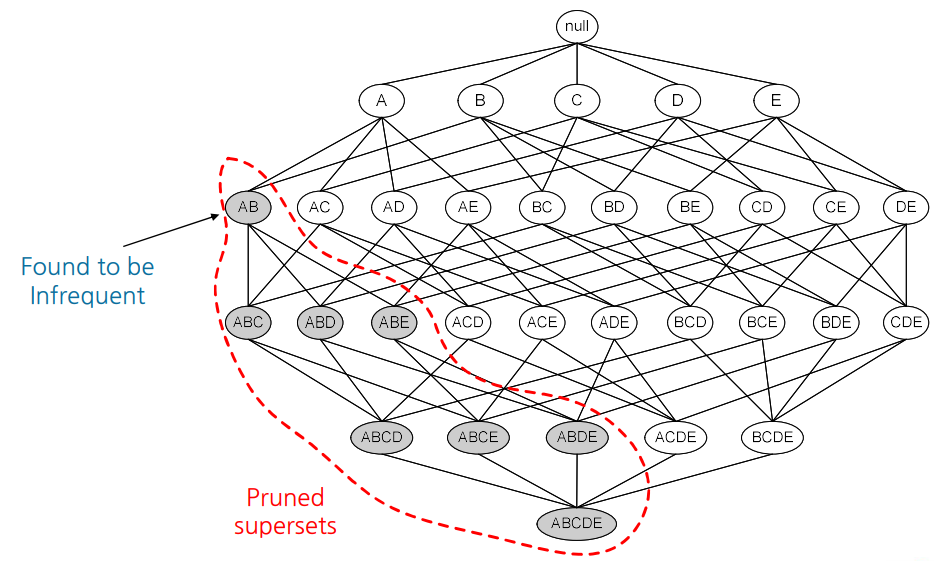
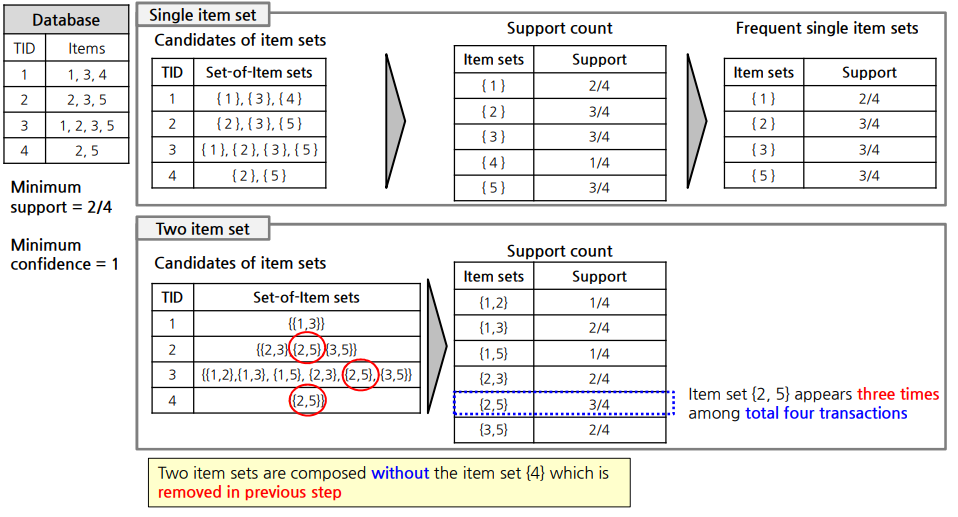
Apriori 원리: 아이템 세트가 빈번한 경우 모든 하위 세트도 빈번하게 있어야 한다.
\[\forall X,Y:(X\subseteq Y) \Rightarrow s(X) \geq s(Y)\]
아이템 세트에 대한 support는 하위 세트에 대한 support를 초과하지 않는다. 이를 안티 모노톤 support 속성이라고 한다.
장점: 병렬화 및 구현이 쉬움
단점: 메모리에 트랜잭션이 다 들어가야함, m번의 데이터베이스 스캔이 필요함
개선책: 해쉬 기반 item set 카운팅, 트랜잭션 나누기

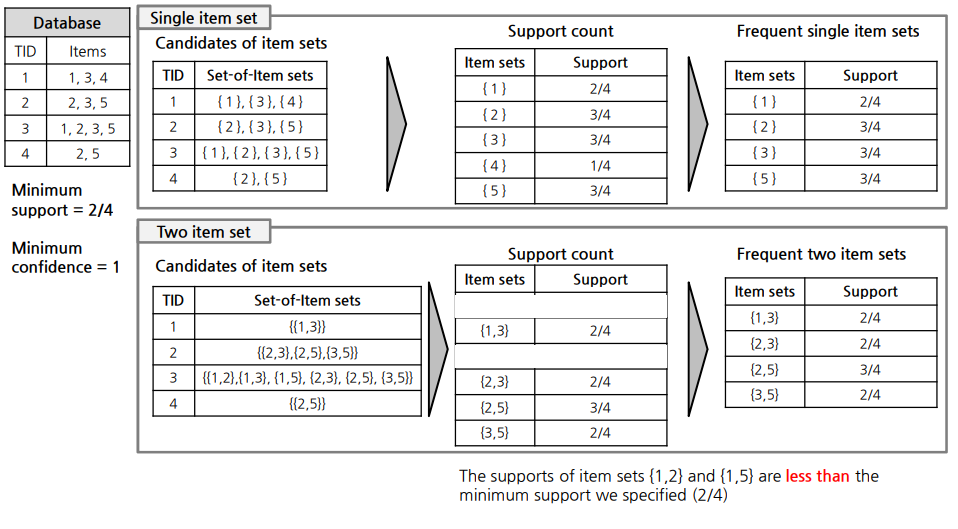
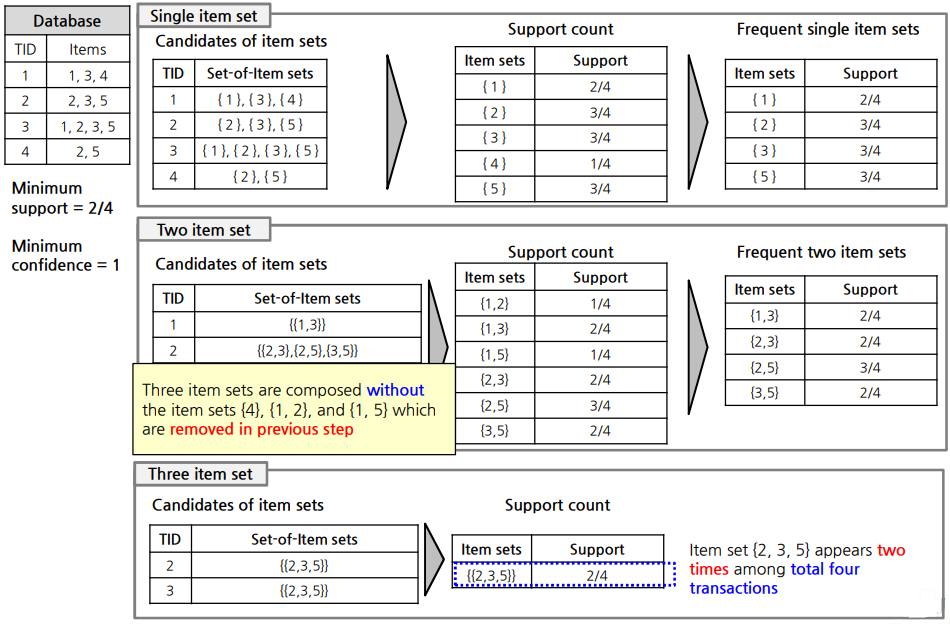
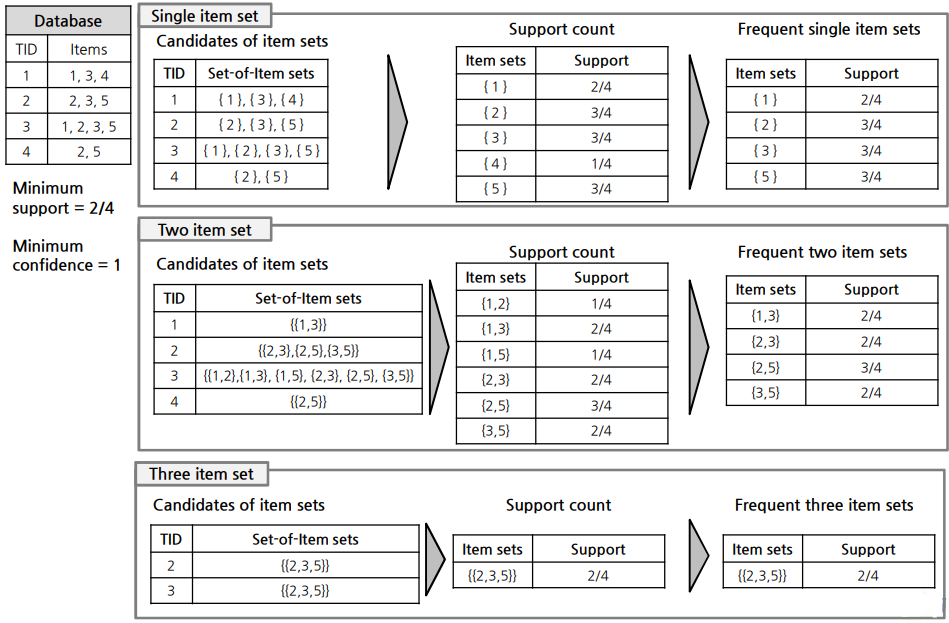
6. Apriori 방법

6.1 Based on support

6.2 Based on confidence

7. FP-growth algorithm

후보 생성 없는 빈번 아이템 세트 탐색 방법
패턴 및 DB 쪼개기를 통해 재귀적으로 빈번 패턴을 키워 나감
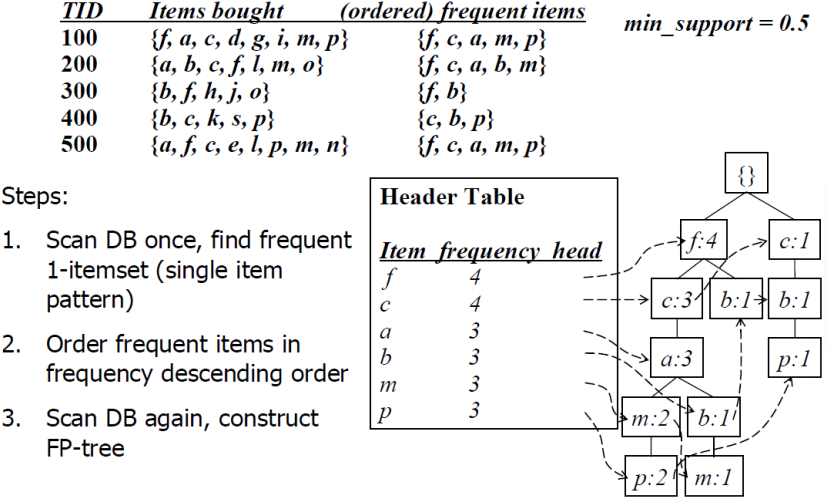
DB를 FP(Frequent Pattern) tree로 구성
알고리즘: 1) 각 빈번 아이템에 대해서 그 projected DB를 생성하고, 그 projected FP-tree를 생성

2) 새로이 생성되는 모든 projected FP-tree에 대해서 프로세스를 수행

3) 결과 FP-tree 가 비거나, 하나의 path만 남을 경우, 그 패스에 대한 모든 조합이 빈번 아이템 집합이 됨

장점: 분할 정복(DB 분해하여 하나에 집중), 후보 생성 및 테스스가 없다, DB가 FP-tree로 압축, 전체 DB 반복 스캔을 피함
단점: FP-tree의 크기가 memory보다 클 가능성이 있다. FP-tree 생성하는 cost가 비싸다.

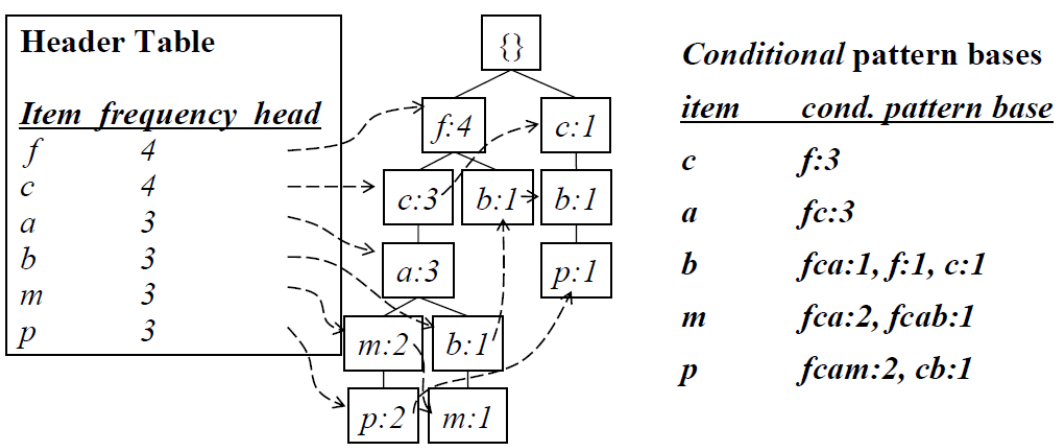
7.1 FP tree

7.2 알고리즘

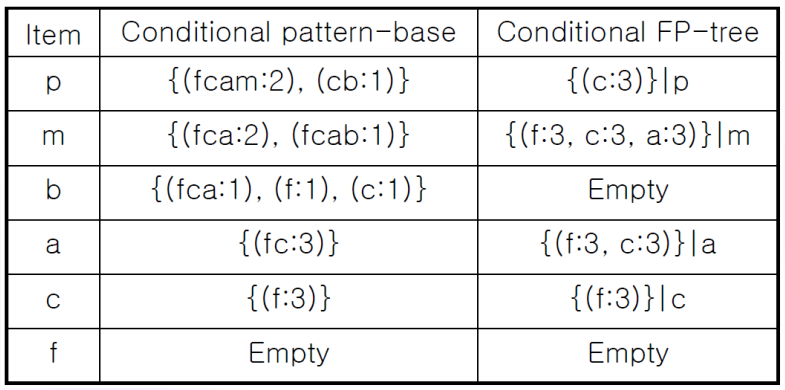
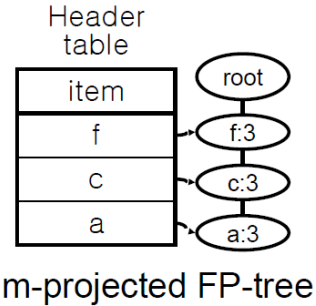
1) 조건부 패턴베이스 만들기

2) 조건부 FP 트리 만들기

3) conditional FP-tree를 재귀적으로 탐색

8. 패턴 평가

연관 규칙 알고리즘은 많은 수의 규칙을 생성할 수 있다.
패턴을 잘라내거나 순위를 매기는데 더 재미있는 방법 사용 가능

8.1 평가 규칙

Confidence가 높아야 한다. ($X \rightarrow Y$)
Confidence($X \rightarrow Y$) > Support($Y$) 그렇지 않으면, 아이템 X를 갖는 것이 실제로 동일한 트랜잭션에서 아이템 Y를 가질 가능성을 감소시키기 때문에 규칙이 잘못된 것

8.2 통계적 독립

Confidence($X \rightarrow Y$) = Support($Y$)

\[\rightarrow P(Y|X)=P(Y) \\ P(X,Y)=P(X) \times P(Y)\]

$if \: P(X,Y) > P(X)\times P(Y)$ : 양의 상관관계

$if \: P(X,Y) < P(X)\times P(Y)$ : 음의 상관관계

8.3 통계적 의존성을 고려한 측정

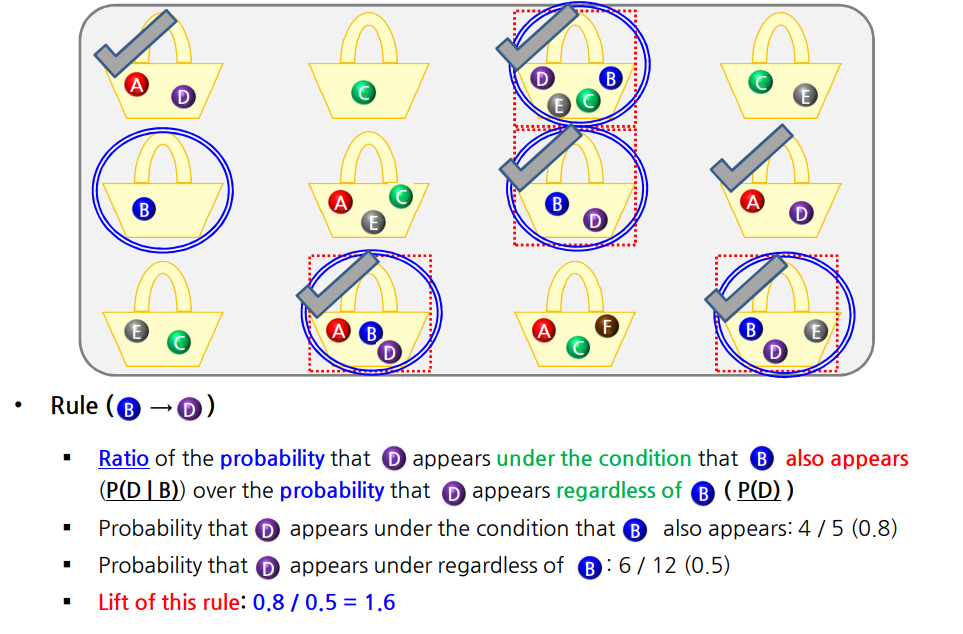
\[lift(X \rightarrow Y)=\frac{confidence(X \rightarrow Y)}{support(Y)}=\frac{P(Y|X)}{P(Y)} = \frac{P(X \cap Y)}{P(X) \cdot P(Y)}\]
$if \: lift(X \rightarrow Y)<1$, 음의 상관관계
$if \: lift(X \rightarrow Y)>1$, 양의 상관관계
$if \: lift(X \rightarrow Y)=1$, 독립