Published: Jun 15, 2020 by Dev-hwon
로지스틱 회귀(Logistic Regression)
- 어떤 사건이 발생할지에 대한 직접 예측이 아니라그 사건이 발생할 확률을 예측
1. Model with a Binary Response Variable
\[y_i=\beta_0+\beta_1x_i, \: y_i=0 \: or \:1\] \[P(y_i=1|x_i)=\pi_i\\P(y_i=0|x_i)=1-\pi_i\] \[E(y_i|X_i)=\sum_{y_i=0\:or\:1}y_iP(y_i|X_i)=1\times+0\times(1-pi_i)=\pi_i\]1.1 응답 변수가 이진일때의 문제점
(1) Normal error term
\[when \: y_i=1,\: \varepsilon_i=1-\beta_0=\beta_1x_i \\ when \: y_i=0,\: \varepsilon_i=-\beta_0=\beta_1x_i\]- 결과적으로, \(\varepsilon_i\)가 정상적으로 분포한다고 가정하는 정상 오차 회귀 모델은 적합하지 않다.
(2) Nonconstant variace of error
\[\text{Given}\:y_i=E(y_i)+\varepsilon_i \:\:\:\:\:\: \begin{matrix} \varepsilon_i=y_i-E(y_i)\\ V(\varepsilon_i)=V(y_i) \end{matrix}\] \[V(y_i)=E\{(y_i-E(y_i))^2\}=\sum_{y_i=0\:or\:1}(y_i-E(y_i))^2\cdot P(y_i) \\ =(1-\pi_i)^2\pi_i+(0-\pi_i)^2(1-\pi_i)\\ =\pi_i(1-\pi_i)\\ =E(y_i)(1-E(y_i))\\ =V(\varepsilon_i)\]- 결과적으로 오차항의 분산은 각 관측치 (상수 분산이 아님)에 따라 달라진다.
(3) Constant on response function
\[E(y_i)=\pi_i \\ 0 \leq E(y_i) \leq 1\]위의 세가지 문제는 일반 선형 회귀 모형에 사용되는 선형 반응 함수를 선택할 때 심각한 문제이다.
일반적으로 반응 변수가 이항인 경우 반응 함수가 비선형이어야 한다는 경험적 증거가 있다.
2. 로지스틱 회귀
- 선형 회귀 개념을 반응 변수가 이진인 상황으로 확장
- 예측 변수 값을 기반으로 클래스를 알 수 없는 새 관측치를 클래스 중 하나로 분류하는데 사용
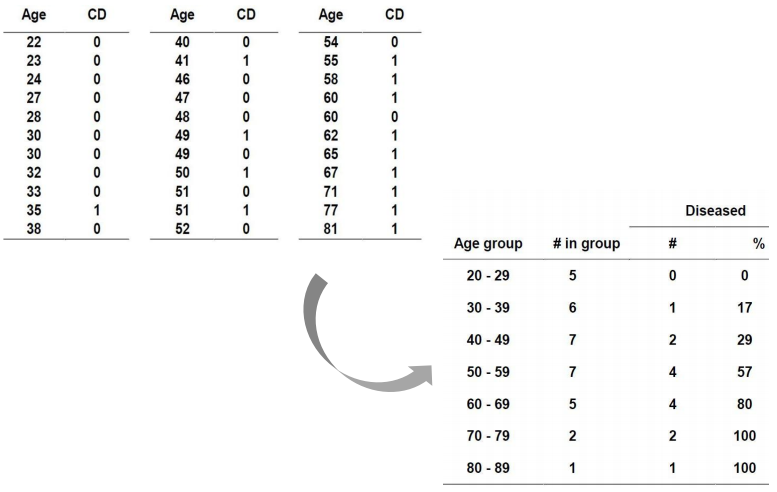
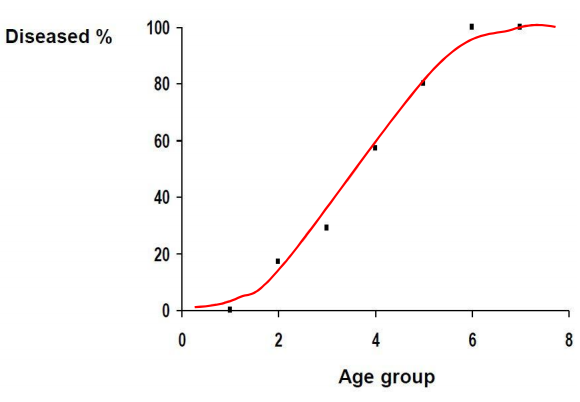
2.1 S-Curve fitting for Classification
- 많은 실제 상황에서 예측 변수의 확률을 S-Curve 모양으로 변경할 수 있다.
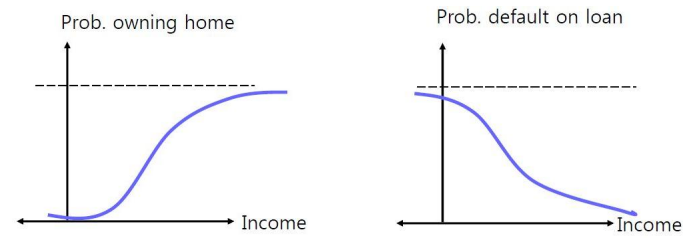
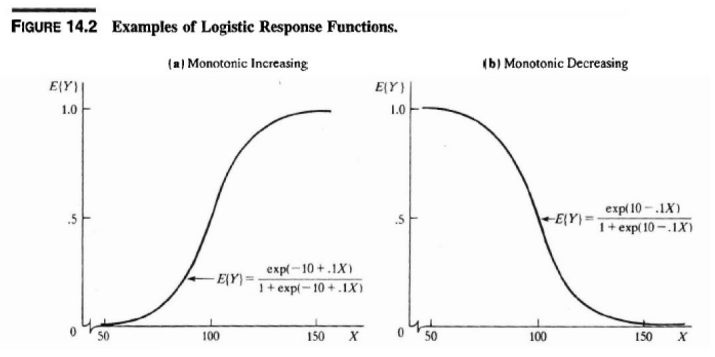
2.2 로지스틱 회귀 모델
- simple logistic regression
2.3 Odds and Logit Transform
- 로지스틱 반응 함수를 정의하려면 먼저 Odds를 정의해야한다.
-
Odds: \(\frac{\pi(X-x)}{1-\pi(X=x)}\:\:\begin{matrix} \rightarrow \text{Probability of belonging to class 1}\\ \rightarrow \text{Probability of belonging to class 0} \end{matrix} \:\:\:\: 0 < Odds < 1\)
-
Odds에 따라 “Logit”을 도출 할 수 있다
2.4 Simple logistic regression & Multiple logistic regression
- Simple logistic regression
- Multiple logistic regression
2.5 로지스틱 회귀 모형의 모수 추정
- 로지스틱 회귀의 모수는 최대 우도 추정 (MLE)으로 얻을 수 있다.
\(\left\{\begin{matrix} P(y_i=1)=\pi_1\\ P(y_i=0)=1-\pi_1 \end{matrix}\right. \:\:\:\: f_i(y_i)=\pi_i^{y_i}(1-\pi_i)^{1-y_i}\) By Bernoulli probability mass function
- 트레이닝 데이터 X의 가능성 및 로그 가능성은 다음과 같이 정의 될 수 있다:
-
MLE : 우리가 보유한 데이터를 얻을 가능성을 최대화하는 추정치를 찾기 위해
-
로지스틱 회귀의 최적 매개 변수는 다음 방정식을 최대화하여 추정 할 수 있다.
ln L은 β의 오목한 함수이다.
ln L을 최대화하는 닫힌 형태의 솔루션은 없다.
최대 가능성 추정값을 계산하기 위해 Numerical search procedures를 사용할 수 있다.
- Iteratively reweight least square
- Newton-Raphson (Gradient Ascent)
- Stochastic gradient ascent
2.6 Fitted Logistic Regression Model
\[\hat{y}=\hat{\pi}(X=x)=\frac{e^{\hat{\beta}^Tx}}{1+e^{\hat{\beta}^Tx}}=\frac{1}{1+e^{-\hat{\beta}^Tx}}\]- 적합 된 로지스틱 회귀 모델을 사용하여 새 객체의 클래스 레이블을 분류 할 수 있다.
- 일반적으로 분류의 컷오프 값은 0.5이다.
2.7 로지스틱 회귀 함수의 기하학적 해석
- 로지스틱 회귀 함수는 p 차원 데이터를 분류하기 위해 (p-1) 차원 초평면으로 간주 될 수 있다.
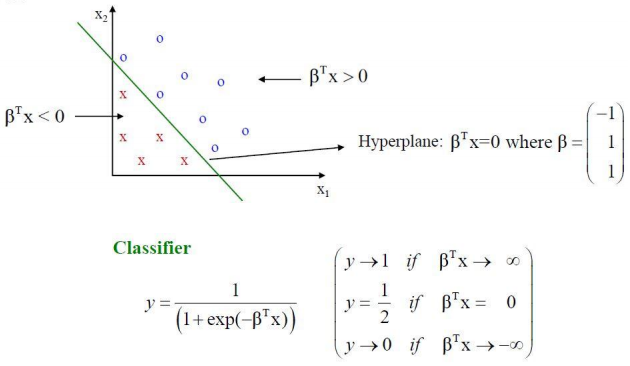
2.8 \(\beta_i\)에 대한 해석
\[\frac{odds(x_1+1,\cdots,x_n)}{odds(x_1,\cdots,x_n}=\frac{e^{\beta_0+\beta_1(x_1+1)+\beta_2x_2+\cdots+\beta_nx_n}}{e^{\beta_0+\beta_1(x_1)+\beta_2x_2+\cdots+\beta_nx_n}}=e^{\beta_1}\]- \(\beta_i\)가 양수일 경우, \(X_i\)는 \(P(y=1)\)와 양의 상관 관계가 있다
- \(\beta_i\)가 음수일 경우, \(X_i\)는 \(P(y=1)\)와 음의 상관 관계가 있다


