Published: Jun 15, 2020 by Dev-hwon
회귀분석(Regression)
- 종속 변수에 영향을 미치는 다수의 독립 변수들과의 관계를 알아보고자 할 때 사용
- 모델의 유의성은 p-value로 판단하는데 p-value 값이 유의수준보다 작을 경우 유의하다고 판단
- 각 독립 변수의 유의성도 마찬가지로 p-value가 유의수준보다 작을 경우 종속 변수 예측에 유의한 영향을 미친다고 판단
- 모델을 얼마나 잘 설명하는지, 즉 모델이 전체 변동을 얼마나 섦명할 수 있는지에 대해서는 결정계수 R-squred를 기준으로 판단(1에 가까울수록 설명력이 높다)
- 다중공산성: 독립 변수들 사이에 강한 상관성이 존재하여 회귀계수 값이 불안정하게 되는 현상
- 분산팽창계수(VIF): 다중공산성을 판단하는 척도, 5이상이면 높고 5이하이면 낮다고 판단
1. 선형 회귀
- 일반적으로 선형 모델은 입력 특성의 가중치 합과 편향(bias 또는 절편)이라sms 상수를 더해 예측을 만든다.
1.1 Two objectives of regression analysis
1) 설명적 모델링: 반응변수(Y)와 예측변수 집합(X)의 관계를 이해하기 위해
2) 예측 모델링: 새로운 사례의 반응 변수 결과를 예측하기 위해
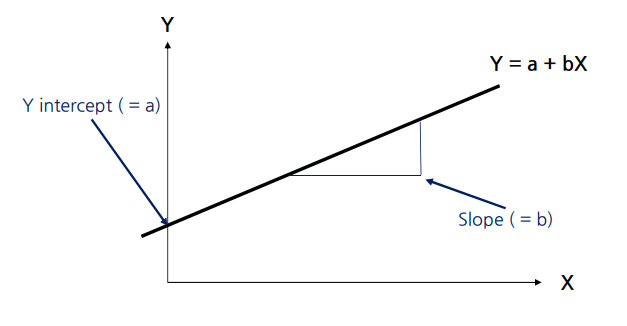
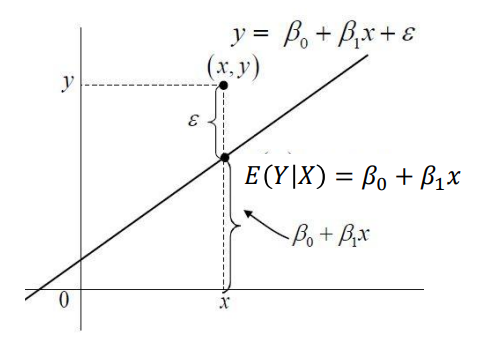
1.2 선형 회귀 모델
\(\varepsilon\)=Random error
랜덤 오차에 대한 가정: \(\varepsilon~N(0,\sigma^2) \rightarrow E(\varepsilon)=0, Var(\varepsilon)=\sigma^2\)
1.3 선형 회귀의 목적
- \(X\)와 \(E(X)\) 사이의 선형 관계를 찾기 위해서
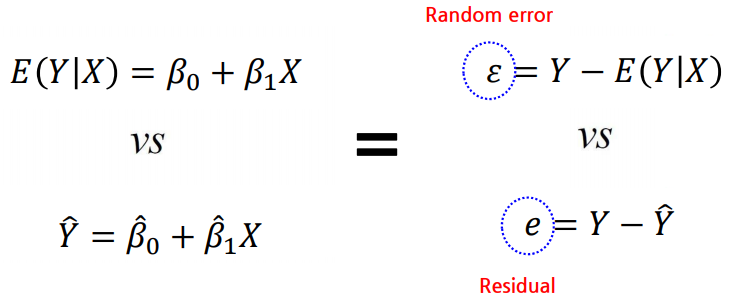
1.4 회귀 모형의 기대치와 적합치의 차이
- 랜덤 오차(\(\varepsilon\))는 관심 수량의 실제 값과 관측 값의 편차
- 잔차(\(e\))는 관심 수량의 관측값과 추정 값의 차이
2. 최소 추정량
2.1 단순 회귀 모형의 최소 추정량
\[\varepsilon_i=y_i-E(y_i)=y_i-(\beta_0+\beta_1x_i)=y_i-\beta_0-\beta_1x_i\] \[Q(\beta_0\beta_1)=\sum^n_{i=1}\varepsilon_i^2=\sum^n_{i=1}(y_i-\beta_0-\beta_1x_i)^2\] \[Minimize\:Q(\beta_0\beta_1)=\sum^n_{i=1}\varepsilon_i^2=\sum^n_{i=1}(y_i-\beta_0-\beta_1x_i)^2\]\(\frac{\partial Q(\beta_0,\beta_1)}{\partial \beta_0}=-2\sum^n_{i=1}(y_i-\beta_0-\beta_1x_i)=0\)
\(\sum y_i-n\beta_0=\beta_1\sum x_i=0\)
\(\hat{\beta_0}=\frac{\sum y_i-\hat{\beta_1}\sum x_i}{n}=\bar{y}-\hat{\beta_1}\bar{x}\)
\[\hat{\beta_0}=\bar{y}-\hat{\beta_1}\bar{x}\] \[\hat{\beta_1}=\frac{\sum{(x_i-\bar{x})(y_i-\bar{y})}}{\sum{(x_i-\bar{x})^2}}\]\(\frac{\partial Q(\beta_0,\beta_1)}{\partial \beta_1}=-2\sum^n_{i=1}(y_i-\beta_0-\beta_1x_i)x_i=0\)
\(\sum x_iy_i-\beta_0\sum x_i-\beta_1\sum(x_i)^2=0\)
\(\sum x_iy_i-(\bar{y}-\hat{\beta_1}\bar{x})\sum x_i-\beta_1\sum(x_i)^2=0\)
\(\sum x_iy_i-\bar{y}\sum x_i-\hat{\beta_1}\bar{x}\sum x_i-\beta_1\sum(x_i)^2=0\)
\(\sum x_iy_i-\bar{y}\sum x_i-\hat{\beta_1}(n\bar{x}^2-\sum(x_i)^2)=0\)
\(\hat{\beta_1}=\frac{n\bar{x}\bar{y}-\sum x_iy_i}{n\bar{x}^2-\sum{(x_i)^2}}=\frac{\sum{(x_i-\bar{x})(y_i-\bar{y})}}{\sum{(x_i-\bar{x})^2}}\)
2.2 다중 선형 회귀에서의 최소 추정량
2.3 최소 제곱 추정의 속성
- Gauss-Markov Theorem: 최소 제곱 추정기는 최고의 선형 비 편향 추정기
- BLUE: 편차가 없고 다른 추정기에 비해 평균 제곱 오차가 가장 작다
3. Unbiases Estimate of \(\sigma^2\)
- 잔차가 정규분포 \(N(0,\sigma^2)\)를 따름
4.회귀계수에 대한 추론
- 계수의 신뢰 구간을 구성하여 계수의 구간 추정
4.1 추정 계수의 분포
\[\hat{\beta}=(X^TX)^{-1}X^TY\] \[E(\hat{\beta})=(X^TX)^{-1}X^TE(Y)=(X^TX)^{-1}X^TX\beta=\beta\] \[V(\hat{\beta})=(X^TX)^{-1}X^TV(Y)X(X^TX)^{-1} \\ = \hat{\sigma}(X^TX)^{-1}X^TX(X^TX)^{-1} \\ = \hat{\sigma}(X^TX)^{-1}\]\(\hat{\beta}\approx N(\beta, \sigma^2(X^TX)^{-1})\) 하지만 실제 분산(\(\sigma^2\))이 알려져 있지 않기 때문 실제 분산 대신 추정 분산에 \(\beta\)의 신뢰 구간을 계산하는 데 사용 \(\hat{\sigma}^2=(\frac{1}{n-k})\sum^n_{i=1}\hat{e}^2_i\)
4.2 계수의 신뢰 구간
- \(\beta_j\)에 대한 대략적인 \(100(1-\alpha)\) 신뢰 구간은 다음과 같이 정의
여기서 \(se(\beta_j)\)는 행렬의 j번째 대각선 요소이다.
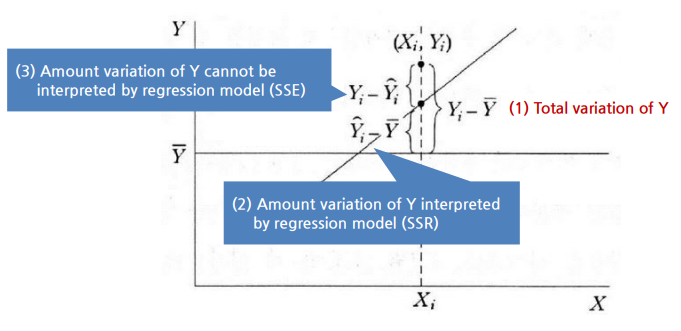
5. 모델의 적합성 판단
- 결정 계수, R2
- 수정된 결정계수, Adjusted R2
5.1 결정 계수, R2
- \(R^2=1\): Y의 전체 변형은 회귀 모형으로 완전히 해석 할 수 있다.
- \(R^2=0\): 회귀 모형이 X와 Y의 관계를 해석 할 수 없다.
5.2 수정된 결정계수, Adjusted R2
- 해당 변수의 기여도 값에 관계없이 모델에 새 X 변수를 추가하면 R2가 항상 증가한다.
- 변수를 추가하면 SSE가 감소하는 경우에 수정된 R2는 증가한다.
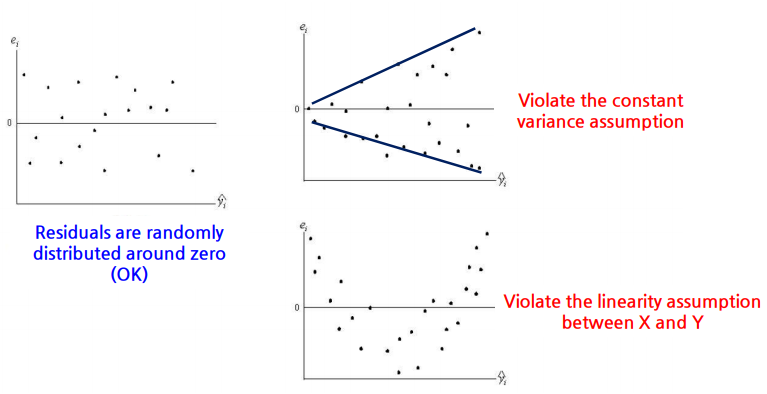
6. 선형 회귀 적용 가정
1) 예측 변수와 반응 변수 사이의 선형성 과정
2) 랜덤 에러가 분산이 일정한지
3) 랜덤 에러의 독립성
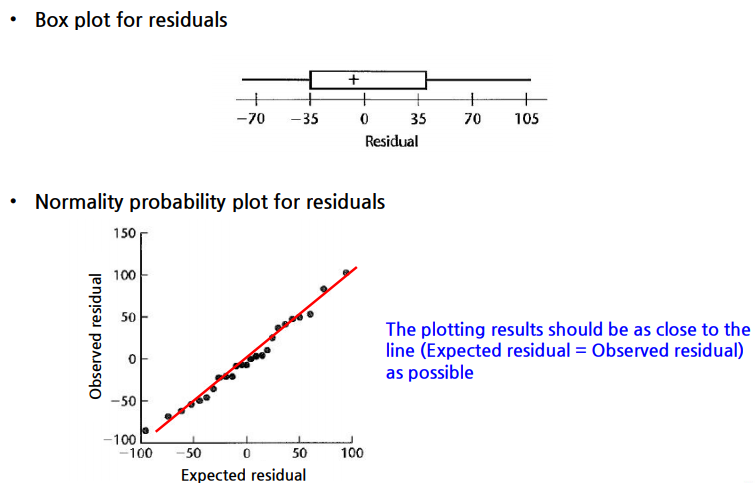
4) 랜덤 에러가 정규분포를 따르는지