비지도 학습

Published: Jun 3, 2020 by Dev-hwon

이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.

비지도 학습(Unsupervised Learning)

입력 특성 \(\mathbf{X}\)는 있지만 레이블 \(\mathbf{y}\)는 없다.
레이블을 붙일 필요 없이 알고리즘이 레이블이 없는 데이터를 바로 사용
군집: 비슷한 샘플을 클러스터로 모은다. 데이터 분석, 고객 분류, 추천 시스템, 검색 엔진, 이미지 분할, 준지도 학습, 차원 축소 등에 사용
이상치 탐지: 정상 데이터가 어떻게 보이는지를 학습하고 비정상 샘플을 감지하는데 사용, 제조 결함 감지나 시계열 데이터에서 새로운 트렌드 찾기
밀도 추정: 데이터셋 생성 확률 과정의 확률 밀도 함수(PDF)를 추정. 이상치 탐지에도 사용. 데이터 분석, 시각화

1. 군집

비슷한 샘플을 구별해 하나의 클러스터 또는 비슷한 샘플의 그룹으로 할당하는 작업
고객 분류: 고객을 구매 이력이나 웹사이트 내 행동 등을 기반으로 클러스터. 추천 시스템
데이터 분석: 데이터셋을 분석할 때 군집 알고리즘을 실행하고 각 클러스터를 따로 분석
차원 축소 기법: 각 클러스터에 대한 샘플의 친화성을 측정. 각 샘플의 특성 벡터 \(\mathbf{x}\)는 클러스터 친화성의 벡터로 바꿀 수 있다. 원본 특성 벡터보다 저차원
이상치 탐지: 모든 클러스터에 친화성이 낮은 샘플은 이상치일 가능성이 높다. 부정 거래 감지에 활용
준지도 학습: 레이블된 샘플이 적을 때 군집을 수행하고 동일한 클러스터에 있는 모든 샘플에 레이블을 전파
검색 엔진: 제시된 이미지와 비슷한 이미지를 찾아준다.
이미지 분할: 색을 기반으로 픽셀을 클러스터로 모으고 각 픽셀의 색을 해당 클러스터의 평균 색으로 변환하며 이미지 색상의 종류를 줄인다. 물체의 윤곽 감지하기 쉬워져 물체 탐지 및 추적시스템에 사용

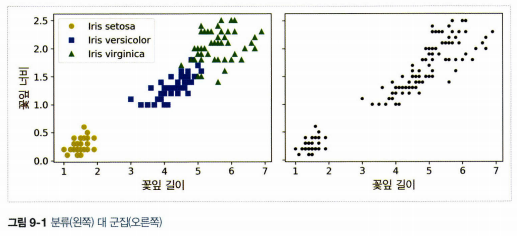
2. k-means

하드 군집: 샘플을 하나의 클러스터에 할당
소프트 군집: 클러스터마다 샘플에 점수를 부여(샘플과 센트로이드 사이의 거리, 가우시안 방사 기저 함수와 같은 유사도 점수 등)
k-means 알고리즘

1) 센트로이드를 랜덤하게 선정

2) 샘플에 레이블을 할당

3) 센트로이드를 업데이트

4) 센트로이드에 변화가 없을 때까지 반복

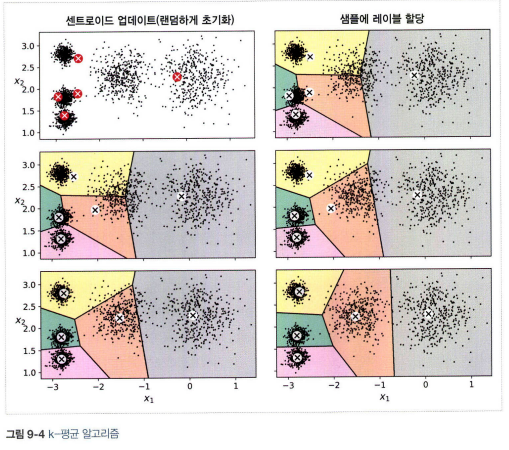
지역 최적점으로 수렴할 수 있다. 센트로이드 초기화가 중요하다.

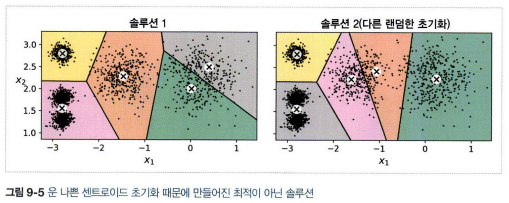
2.1 센트로이드 초기화 방법

첫번째 방법: 센트로이드 위치를 근사하게 알 수 있는 경우 그 위치로 초기화(다른 군집 알고리즘을 먼저 실행)
두번째 방법: 랜덤 초기화를 다르게 하여 여러 번 알고리즘을 실행하고 가장 좋은 솔루션 선(각 샘플과 가장 가까운 센트로이드 사이의 평균 제곱 거리인 이너셔를 이용)

2.2 k-means++ 알고리즘

다른 센트로이드와 거리가 먼 센트로이드를 선택하는 초기화 단계 이용
방법

1) 데이터셋에서 무작위로 균등하게 하나의 센트로이드 \(\mathbf{c}^{(1)}\) 선택

2) \(D(\mathbf{x}^{(i)})^2/\sum^m_{j=1}D(\mathbf{x}^{(j)})^2\)의 확률로 샘플 \(\mathbf{x}^{(i)}\)를 새로운 센트로이드 \(\mathbf{c}^{(i)}\)로 선택(\(D(\mathbf{x}^{(i)})\)는 샘플 \(\mathbf{x}^{(i)}\))와 이미 선택된 가장 가까운 센트로이드까지 거리, 이 확률 분호는 이미 선택한 센트로이드에서 멀리 떨어진 샘플을 다음 센트로이드로 선택할 가능성을 높임)

3) k개의 센트로이드가 선택 될 때까지 반복

2.3 k-means 속도 개선과 미니배치 k-means

삼각 부등식을 사용하여 속도를 개선하고 샘플과 센트로이드 사이의 거리를 위한 하한선과 상한선을 유지
미니배치 k-means: 전체 데이터셋을 사용하여 반복하지 않고 각 반복마다 미니배치를 사용해 센트로이드를 이동. 대량의 데이터셋에 적용 가능. 일반 k-means보다 빠르지만 이너셔는 일반적으로 조금 나쁨.(특히 클러스터 개수 증가할 때)

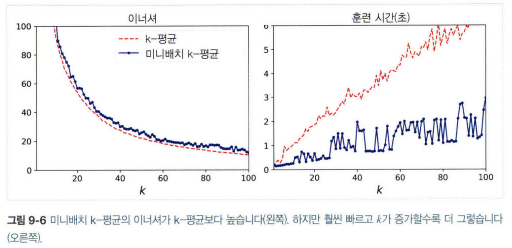
2.4 최적의 클러스터 개수 찾기

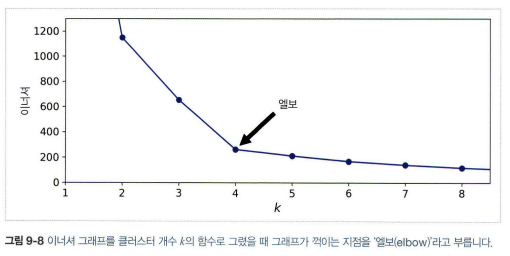
이너셔는 k가 증가함에 따라 점점 작아지므로 k를 선택할 때 좋은 지표가 아니다.
이너셔로 k 선택할 때는 엘보우 지점에서 선택

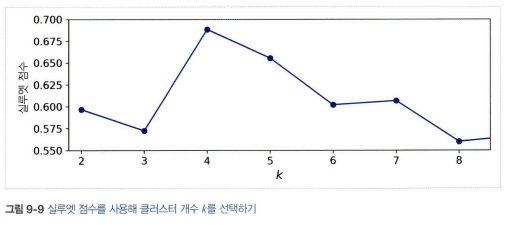
더 좋은 방법으로는 실루엣 점수(모든 샘플에 대한 실루엣 계수의 평균)
실루엣 계수: \((b-a)/max(a,b)\) (\(a\)는 클러스터 내부의 평균 거리, \(b\)는 가장 가까운 클러스터까지 평균 거리)
실루엣 계수가 +1에 가까우면 자신의 클러스터 안에 잘 속해 있고 다른 클러스터와 멀리 떨어져 있다는 뜻

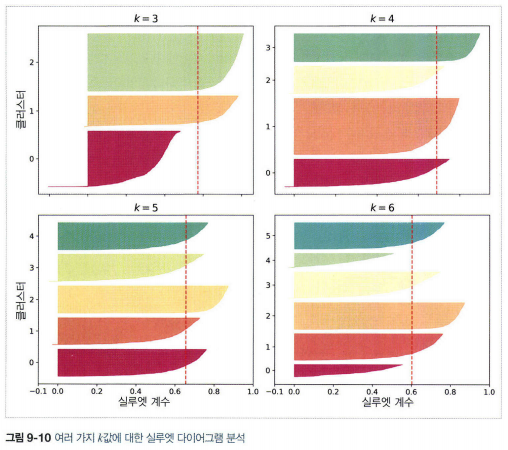
실루엣 다이어그램: 높이는 클러스터안 샘플의 개수, 너비는 클러스터안 샘플의 정렬된 실루엣 계수(넓을 수록 좋음), 수직 파선은 각 클러스터 개수에 해당하는 실루엣 점수
샘플들의 계수가 전반적으로 높고, 모든 클러스터 크기가 비슷한게 좋다.

2.5 k-means의 한계

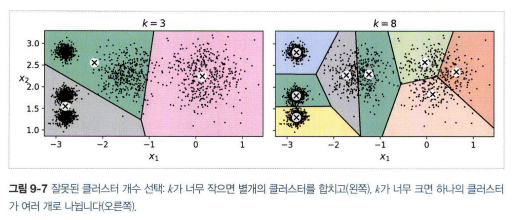
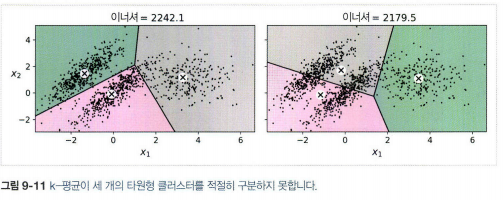
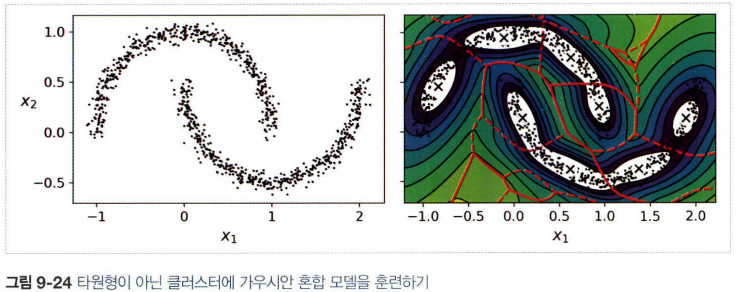
알고리즘을 여러 번 실행해야하고, 클러스터 개수를 지정해야한다. 클러스터의 크기나 밀집도가 서로 다르거나 원형이 아닐 경우 잘 작동하지 않는다.

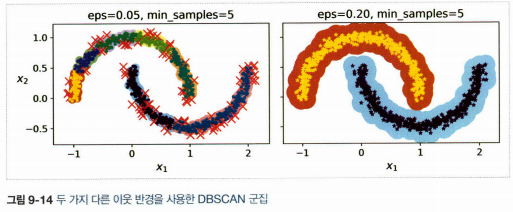
3. DBSCAN

밀집된 연속적 지역을 클러스터로 정의
방법

1) 알고리즘이 각 샘플에서 작은 거리인 \(\varepsilon\)(입실론) 내에 샘플이 몇 개 놓여 있는지 센다. 이 지역을 샘플의 \(\varepsilon\)-이웃이라고 한다.

2) (자신 포함)\(\varepsilon\)-이웃 내에 적어도 min_samples개 샘플이 있다면 이를 핵심 샘플로 간주한다.

3) 핵심 샘플의 이웃에 있는 모든 샘플은 동일한 클러스터에 속한다.

4) 핵심 샘플이 아니고 이웃도 아닌 샘플은 이상치로 판단

장점	단점
* 매우 간단, 강력 * 클러스터의 모양과 개수에 상관없이 감지 * 이상치에 안정적 * 하이퍼파라미터가 2개뿐	* 클러스터간의 밀집도가 크게 다르면 모든 클러스터를 올바르게 잡아내는 것이 불가능 * 계산 복잡도 \(O(m log m)\) * 사이킷런 구현은 eps가 커지면 \(O(m^2)\)만큼 메모리가 필요

4. 다른 군집 알고리즘

병합 군집: 클러스터 계층을 밑바닥부터 위로 쌓아 구성, 반복마다 병합 군집은 인접한 클러스터 쌍을 연결. 대규모 샘플과 클러스터에 잘 확장, 다양한 형태의 클러스터를 감지, 특정 클러스터 개수를 선택하는데 도움이 되는 클러스터 트리를 만들 수 있다. 연결 행렬이 없으면 대규모 데이터셋으로 확장이 어렵다.
BIRCH: 대규모 데이터셋을 위해 고안. 훈련 과정에서 새로운 샘플을 클러스터에 빠르게 할당할 수 있는 정보를 담은 트리 구조 생성. 제한된 메모리를 사용해 대용량 데이터셋 사용
평균-이동: 각 샘플을 중심으로 하는 원을 그리고 각 원마다 포함된 모든 샘플의 평균을 구한 뒤 원의 중심을 평균점으로 이동. 원이 움직이지 않을 때까지 반복. 지역의 최대 밀도를 찾아 원을 이동. 모양이나 개수에 상관없이 클러스터를 차아내고 하이퍼파라미터도 적다. DBSCAN과 달리 클러스터 내부 밀집도가 불균형할 때 여러 개로 나누는 경향이 있으며 계산 복잡도는 \(O(m^2)\)
유사도 전파: 투표 방식 사용. 각 샘플이 자신을 대표할 수 있는 비슷한 샘플에 투표하여 각 대표와 투표한 샘플이 클러스터를 형성. 크기가 다른 여러 개의 클러스터를 감지. 계산 복잡도 \(O(m^2)\)
스펙트럼 군집: 샘플 사이의 유사도 행렬을 받아 저차원 임베딩을 생성, 저차원 공간에서 또 다른 군집 알고리즘을 사용. 복잡한 클러스터 구조를 감지하고 그래프 컷을 찾는데 사용 가능. 샘플 개수가 많으면 잘 적용되지 않고 클러스터의 크기가 매우 다르면 잘 작동하지 않음.

5. 가우시안 혼합

샘플이 파라미터가 알려지지 않은 여러 개의 혼합된 가우시안 분포에서 생성되었다고 가정하는 확률 모델
데이터셋 \(\mathbf{x}\) 가정

1) 샘플마다 \(k\)개의 클러스터에서 랜점하게 한 클러스터가 선택. \(j\)번째 클러서터를 선택할 확률은 클러스터의 가중치 \(\phi^{(j)}\)로 정의의. \(i\)번째 샘플을 위ㅟ해 선택한 클러스터 인덱스는 \(z^{(i)}\)로 표시

2) \(z^{(i)}=j\)(\(i\)번째 샘플이 \(j\)번째 클러스터에 할당)이면 이 샘플의 위치 \(\mathbf{x}^{(i)}\)는 평균이 \(\mu^{(j)}\)이고 공분산 행렬이 \(\sum^{(j)}\)인 가우시안 분포에서 랜덤하게 샘플링(\(\mathbf{x}^{(i)}~\mathbf{N}(\mu^{(j), \sum^{(j)}})\))

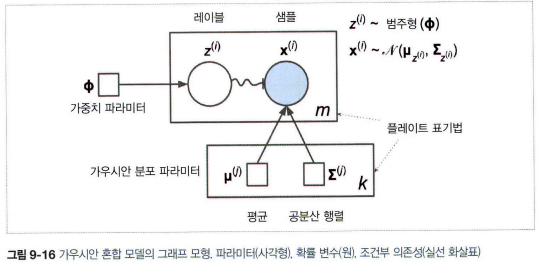
원은 확률 변수

사각형은 고정값(모델의 파라미터)

큰 사각형은 플레이트. 안의 내용이 여러번 반복

각 플레이트 오른쪽 아래 숫자는 안의 내용이 얼마나 반복되는지 표현.

각 변수 \(z^{(i)}\)는 가중치 \(\phi\)를 갖는 범주형 분포에서 샘플링. 각 변수 \(\mathbf{x}^{(i)}\)는 해당하는 클러스터 \(z^{(i)}\)로 정의된 평균과 공분산 행렬을 사용해 정규분포에서 샘플링

실선 화살표는 조건부 의존성을 표현. 화살표가 플레이트 경계를 가로지르면 해당 플레이트의 모든 반복에 적용

\(z^{i)}\)에서 \(\mathbf{x}^{(i)}\)까지 구불구불한 화살표는 스위치. \(z^{i)}\)의 값에 따라 샘플 \(\mathbf{x}^{(i)}\)가 다른 가우시안 분포에서 샘플링

색이 채워진 원은 알려진 값(관측 변수, 알려지지 않은 값은 잠재 변수)

기댓값-최대화 알고리즘(EM): 샘플을 각 클러스터에 속할 확률을 예측하여 클러스터에 할당(기댓값 단계), 데이터 셋에 있는 모든 샘플을 사용하여 클러스터를 업데이트(최대화 단계). k-means와 다르게 소프트 클러스터 할당을 사용.

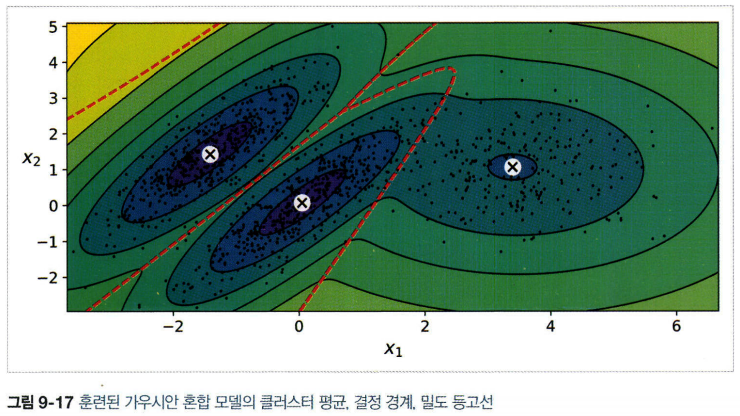
특성이나 클러스터가 많거나 샘플이 적을 때는 EM이 최적의 솔루션으로 수렴하기 어렵다.
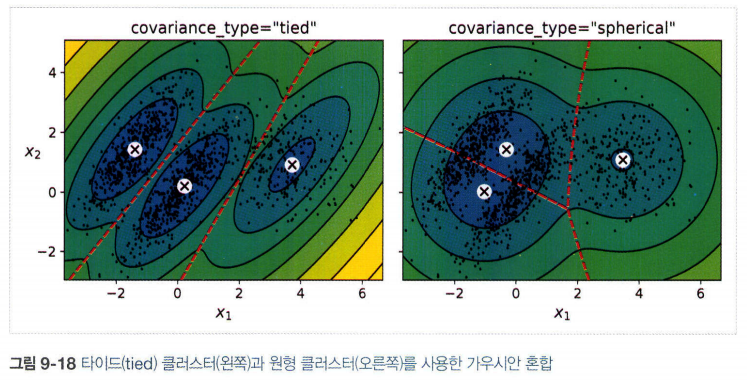
공분산 행렬에 제약을 추가하는 방법(covariance_type 매개변수)

1) “spherical”: 모든 클러스터가 원형. 지름은 다를 수 있다.(분산이 다르다)

2) “diag”: 크기 상관없이 어떤 타원형도 가능하다. 하지만 타원의 축은 좌표 축과 나란해야 한다.(공분산 행렬이 대각행렬)

3) “tied”: 모든 클러스터가 동일한 타원 모양, 크기, 방향을 가진다.(클러스터들이 동일한 공분산 행렬을 공유)

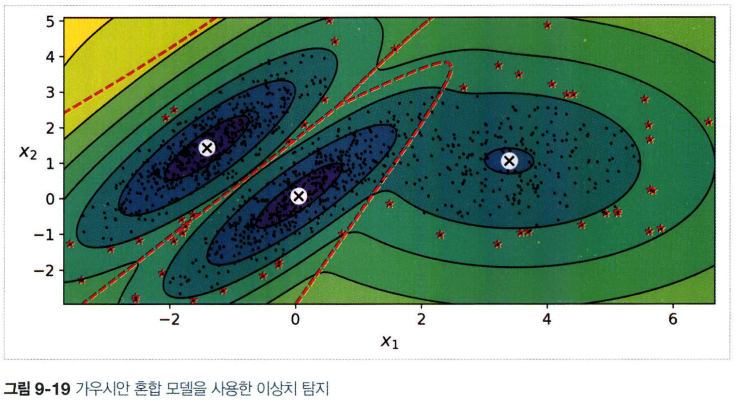
5.1 가우시안 혼합을 사용한 이상치 탐지

밀도 임계값을 정하여 밀도가 낮은 지역에 있는 모든 샘플을 이상치로 가정
깨끗한 데이터셋에서 특이치 탐지로 사용도 가능

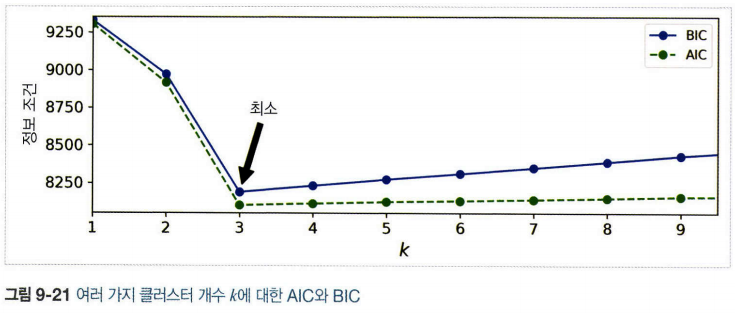
5.2 클러스터 개수 선택

이너셔나 실루엣 점수 같은 지표 사용 불가능(클러스터가 타원형이거나 크기가 다를 때 안정적이지 않다)
BIC(Bayesian information criterion)나 AIC(Akaike information criterion) 같은 이론적 정보 기준을 최소화 하는 모델을 찾는다.

BIC와 AIC

\(BIC = log(m)p-2log(\hat{L})\)
\(AIC = 2p-2log(\hat{L})\)

\(m\)은 샘플의 개수

\(p\)는 모델이 학습할 파라미터 개수

\(\hat{L}\)은 모델의 가능도 함수의 최댓값

두 가지 모두 학습할 파라미터가 많은 모델(클러스터가 많은)에게 벌칙을 가하고 데이터에 잘 학습하는 모델에게 보상
두 가지 모두 동일한 모델을 선택하는 경향이 있지만, 다른 모델이 선택되는 경우 BIC가 AIC보다 간단한 모델을 선택하는 경향이 있다.(데이터에 아주 잘 맞지 않을 수 있다. 특히 대규모 데이터셋에서)
가능도 함수: 확률은 파라미터 \(\theta\)인 모델이 주어지면 미래 출력 \(\mathbf{x}\)가 얼마나 그럴듯한지 설명하는 것이라면 가능도는 출력 \(\mathbf{x}\)를 알고 있을 때 파라미터 \(\theta\)가 얼마나 그럴듯한지 설명

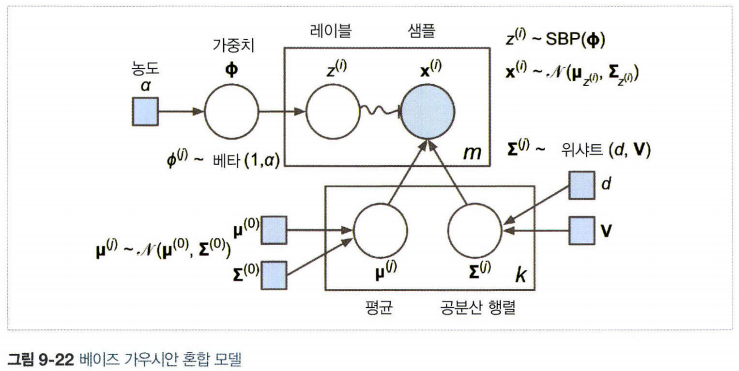
6. 베이즈 가우시안 혼합 모델

최적의 클러스터 개수를 수동으로 찾지 않고 불필요한 클러스터의 가중치를 0또는 0에 가깝게 만드는 방법
클러스터 개수 n_componets를 최적의 클러스터 개수보다 크다고 믿을 만한 값을 지정하고 불필요한 클러스터를 제거하는 방법
클러스터 파라미터(가중치, 평균, 공분산 행렬 등)는 고정된 모델 파라미터가 아닌 잠재 확률 변수로 취급
베타분포: a 와 b라는 두 모수를 가지며 표본 공간은 0과 1사이의 실수다. 즉 0과 1 사이의 표본값만 가질 수 있다. 고정 범위 안에 놓인 값을 가진 확률 변수를 모델링 할 때 자주 사용. (참고: https://datascienceschool.net/view-notebook/70a372b9c14a4e8d9d49737f0b5a3c97/)

타원형 클러스터에 잘 작동하나 다른 모양을 가진 데이터셋에는 좋지 못하다.

7. 이상치 탐지와 특이치 탐지를 위한 다른 알고리즘을

PCA(그리고 inverse_transform() 메서드를 가진 다른 차원 축소 기법): 샘플의 재구성 오차와 이상치의 재수겅 오차를 비교하면 일반적으로 후자가 크다. 이를 이용하여 이상치 탐지
Fast-MCD(minimum covariance determinant): EllipticEnvelope 클래스에서 구현. 데이터셋을 정제할 때 사용. 샘플(정상치)가 하나의 가우시안 분포에서 생성되었다고 가정하고 이 가우시안 분포에서 생성되지 않은 이상치로 이 데이터셋이 오염되었다고 가정. 가우시안 분포의 파라미터를 추정할 때 이상치로 의심되는 샘플을 무시
아이솔레이션 포레스트: 고차원 데이터셋에서 이상치 감지를 위한 알고리즘. 무작위로 성장한 결정 트리로 구성된 랜덤 포레스트 생성. 모든 샘플이 다른 샘플과 격리될 때까지 진행하고 다른 샘플과 멀리 떨어져있는 샘플을 이상치로 판단. 평균적으로 정상 샘플과 적은 단계에서 격리
LOF(local outlier factor): 주어진 샘플 주위의 밀도와 이웃 주위의 밀도를 비교
one-class SVM: 특이치 탐지에 사용. SVM이지만 클래스가 하나. 원본 공간으로부터 고차원 공간에 있는 샘플을 분리(원본 공간에서는 모든 샘플을 둘러싼 작은 영역을 찾는 것). 새로운 샘플이 이 영역 안에 놓이지 않는 다면 이는 이상. 고차원 데이터셋에 잘 작동하나 대규모 데이터셋으로 확장은 어렵다.