차원 축소

Published: Jun 2, 2020 by Dev-hwon

이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.

차원 축소(Dimensionality Reduction)

PCA, 커널 PCA, LLE 등

장점	단점
* 특성 수를 줄여 훈련 속도를 높일 수 있다. * 잡음이나 불필요한 세부사항을 걸러내 성능을 높일 수 있다. * 데이터 시각화에도 유용하다.	* 일부 정보가 유실된다.(성능이 조금 나빠질 수 있다.) * 작업 파이프라인이 더 복잡하게 되고 유지 관리가 어려워진다.

차원 축소 관련 더 자세한 내용 보러 가기

1. 차원의 저주

차원의 저주: 많은 특성은 훈련을 느리게 하고, 좋은 솔루션을 찾기 어렵게 한다.
고차원 초입방체에 있는 대다수의 점은 경계와 매우 가까이 있다.
고차원으로 갈수록 데이터간의 거리가 멀어진다. 따라서 예측을 위해 춸씬 많은 외삽을 해야하기 때문에 저차원일 때보다 예측이 더 불안정하다. (과대적합 위험이 커짐)
해결책으로는 훈련 샘플의 밀도가 충분히 높아질 때까지 훈련 세트의 크기를 키우는 것(일정 밀도에 도달하기 위해 필요한 샘플 수는 차원 수가 커짐에 따라 기하급수적 증가)

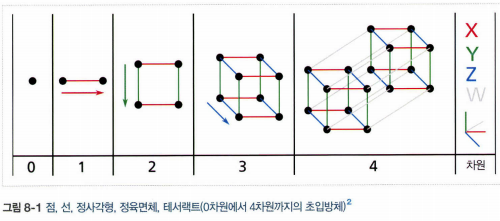
2. 차원 축소를 위한 접근 방법

투영, 매니폴드 학습

2.1 투영

많은 특성은 거의 변화가 없는 반면, 다른 특성들은 서로 강하게 연관되어 있다.
모든 훈련 샘플이 고차원 공간 안의 저차원 부분 공간에 놓여 있다.

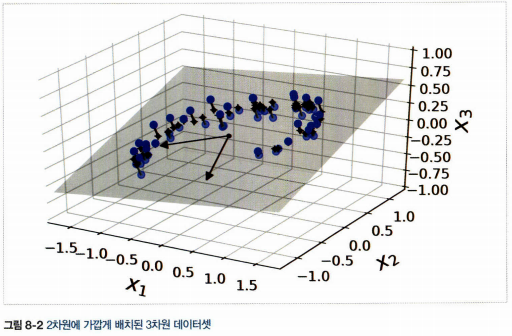
모든 훈련 샘플을 저차원 부분 공간에 수직으로 투영하면 차원이 축소된 데이터 셋을 얻을 수 있다.

스위스 롤 데이터셋처럼 부분 공간이 뒤틀리거나 휘어 있는 경우 투영이 최선의 방법은 아니다.

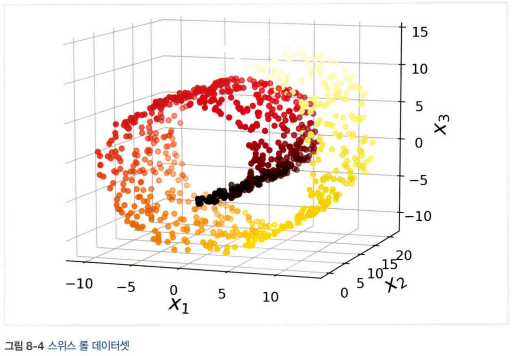
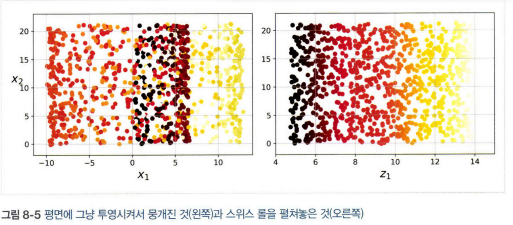
2.2 매니폴드 학습

스위스 롤은 2D 매니폴드의 한 예
d차원 매니폴드: d차원 초평면으로 보일 수 있는 n차원 공간의 일부(d<n)
매니폴드 학습: 실제 고차원 데이터셋이 더 낮은 저차원 매니폴드에 가깝게 놓여 있다는 매니폴드 가정 또는 매니폴드 가설에 근거하여 매니폴드를 모델링 하는 방법
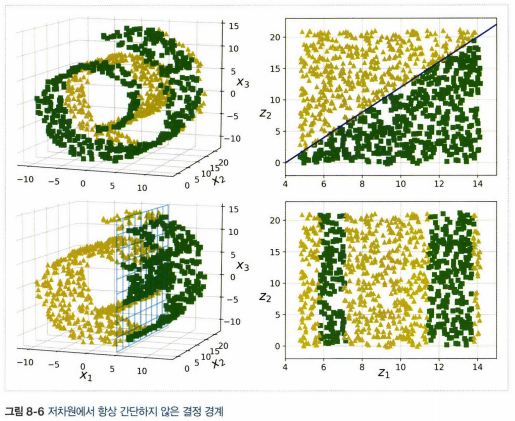
매니폴드 가정은 처리해야 할 작업이 저차원의 매니폴드 공간에 표현되면 더 간단해질 것이라는 가정과 병행. 이 가정이 항상 유효하지는 않음

3. 주성분 분석(PCA)

데이터에 가장 가까운 초평면을 정의한 다음, 데이터를 초평면에 투영시키는 방법

3.1 분산 보존

초평면에 훈련 세트를 투영하기 전에 올바른 초평면을 선택해야 한다.
올바른 초평면: 다른 방향으로 투영하는 것보다 분산이 최대로 보존되는 축을 선택하는 것이 정보가 가장 적게 손실되므로 합리적(원본 데이터셋과 투영된 것 사이의 평균 제곱 거리를 최소화)

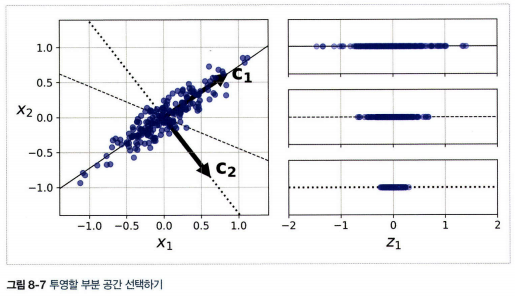
3.2 주성분

고차원 데이터셋을 분산이 최대인 축을 계속 찾아가며 축소하는 경우 i번째 축을 이 데이터의 i번째 주성분(PC)라고 한다.
주성분을 찾는 방법은 특잇값 분해(SVD)라는 표준 행렬 분해 기술을 이용한다.
특잇값 분해(SVD): 훈련 세트 행렬 X를 세 개 행렬의 행렬 곱셈인 \(\mathbf{U}\sum\mathbf{V}^T\)로 분해 할 수 있다.

주성분 행렬

\[\mathbf{V} = \begin{pmatrix} |& | & & |\\ c_1& c_2 & \cdots & c_n\\ | & | & & | \end{pmatrix}\]

3.3 d차원으로 투영하기

주성분을 추출 후 d개의 주성분으로 정의한 초평면에 투영하여 데이터 셋을 d차원으로 축소
d차원으로 축소된 데이터셋 \(\mathbf{X}^{d-proj}\)을 얻기 위해서는 행렬 \(\mathbf{X}\)와 \(\mathbf{V}\)의 첫 d열로 구성된 행렬 \(\mathbf{W}_d\)를 행렬 곱셈한다.

훈련 세트를 d차원으로 투영하기

\[\mathbf{X}_{d-proj}=\mathbf{X}\mathbf{W}_d\]

3.4 적절한 차원 수 선택하기

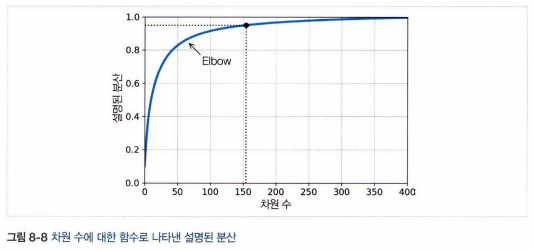
차원 수를 임의로 정하기보다는 충분한 분산(예 95%)이 될 때까지 더해야 할 차원 수를 선택하는 것이 간단(시각화는 2, 3차원으로)
다른 방법은 설명된 분산을 차원 수에 대한 함수로 그리는 것(변화가 크지 않는 변곡점)

3.5 압축을 위한 PCA

차원을 축소하고 난 후에는 훈련 세트 크기 감소 -> 알고리즘 속도 상승
압축된 데이터셋에 PCA 투형의 변환을 반대로 적용하여 차원을 되돌릴 수도 있다.(투영에서 일정량 정보를 잃었기 때문에 원본 데이터셋은 얻을 수 없다. but 매우 비슷)
원본데이터와 재구성된 데이터 사이의 평균 제곱 거리를 재구성 오차라고 한다.

3.6 랜덤 PCA

확률적 알고리즘을 사용해 처음 d개의 주성분에 대한 근삿값을 빠르게 찾는다.
계산 복잡도는 \(O(m \times d^2)+O(d^3)\)(완전한 SVD 방식은 \(O(m \times n^2)+O(n^3)\), d가 n보다 작으면 완전 SVD보다 빠르다.)

3.7 점진적 PCA

PCA 구현의 문제는 SVD 알고리즘을 실행하기 위해 전체 훈련 세트를 메모리에 올려야 한다는 것
점진적 PCA(IPCA): 훈련 세트를 미니배치로 나눈 뒤 IPCA 알고리즘에 한 번에 하나씩 주입(훈련 세트가 클 때 유용, 온라인 PCA 적용 가능)

4. 커널 PCA(kPCA)

샘플을 매우 높은 고차원 공간(특성 공간)으로 암묵적으로 매핑하는 커널 기법을 PCA에 적용하여 차원 축소를 위한 복잡한 비선형 투형을 수행
투영된 후에 샘플의 군집을 유지하거나 꼬인 매니폴드에 가까운 데이터셋을 펼칠 때도 유용

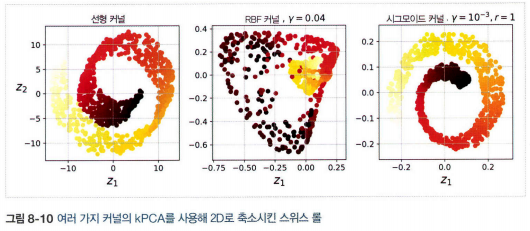
4.1 커널 선택과 하이퍼파라미터 튜닝

그리드 탐색을 사용하여 주어진 문제에서 성능이 가장 좋은 커널과 하이퍼파라미터를 선택
완전한 비지도 학습 방법으로, 가장 낮은 재구성 오차를 만드는 커널과 하이퍼파라미터를 선택하는 방식도 있다.(but 선형 PCA만큼 재구성은 쉽지 않다.)

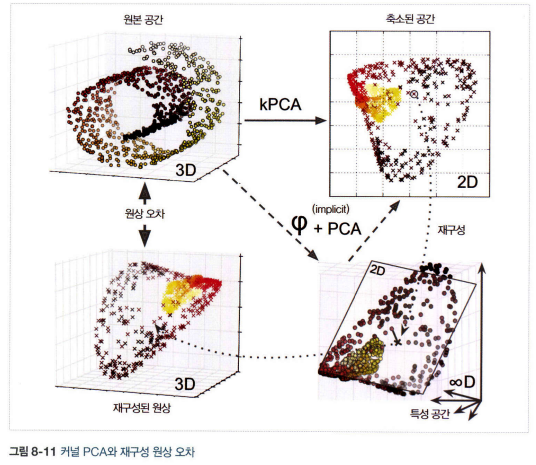
위 그림은 원본 3D 데이터셋(왼쪽 위)과 RBF 커널의 kPCA를 적용한 2D 데이터셋(오른쪽 위), 커널 트릭 덕분에 특성 맵 \(\varphi\)를 사용하여 훈련 세트를 무한 차원의 특성 공간으로 매핑, 변환된 데이터셋을 선형 PCA를 사용해 2D로 투영(오른쪽 아래)
축소된 공간에 잇는 샘플에 대해 선형 PCA를 역전시키면 재구성된 데이터 포인트는 원본 공간이 아닌 특성 공간에 놓인다(왼쪽 아래)
특성 공간은 무한 차원이기 때문에 재구성된 포인트를 계산할 수 없고 재구성에 따른 실제 에러를 계산할 수 없다.
but 재구성된 포인트에 가깝게 매핑된 원본 공간의 포인트를 찾을 수 있다. 이를 재구성 원상이라고 한다.
재구성 원상을 이용하여 원본 샘플과의 오차를 최소하하는 커널과 하이퍼파라미터 선택 가능

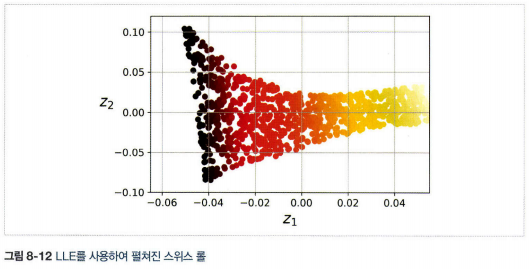
5. 지역 선형 임베딩(LLE)

강력한 비선형 차원 축소
매니폴드 학습
방법:

1) 각 훈련 샘플 \(\mathbf{x}^{(i)}\)에 대해 가장 가까운 k개의 샘플을 찾는다.

2) 이 이웃에 대한 선형 함수로 \(\mathbf{x}^{(i)}\)를 재구성한다. (\(\mathbf{x}^{(i)}\)와 \(\sum^m_{j=1}w_{i,j}\mathbf{x}^{(i)}\) 사이의 제곱 거리가 최소가 되는 \(w_{i,j}\)를 찾는 것, \(\mathbf{W}\)는 가중치 \(w_{i,j}\)를 모두 담은 가중치 행렬)

선형적인 지역 관계 모델링

\[\hat{\mathbf{W}}=\underset{\mathbf{w}}{argmin}\sum^{m}_{i=1}(\mathbf{x}^{(i)}-\sum^m_{j=1}w_{i,j}\mathbf{x}^{(i)})^2\]

[조건] \(\left\{\begin{matrix} w_{i,j}=0 & \mathbf{x}^{(j)}가 \mathbf{x}^{(i)}의 최근접 이웃 k개 중 하나가 아닐 때 \\ \sum^m_{j=1}w_{i,j}=1 & i=1,2,\cdots, m일 때 \end{matrix}\right.\)

3) 가능한 이 관계가 보존되도록 훈련 샘플을 d차원 동간(d<n)으로 매핑, 만약 \(\mathbf{z}^{(i)}\)가 d차원 공간에서 \(\mathbf{x}^{(i)}\)의 상이라면 가능한 \(\mathbf{z}^{(i)}\)와 \(\sum^m_{j=1}\hat{w}_{i,j}\mathbf{z}^{(j)}\) 사이의 거리가 최소화 되어야 한다.(\(\mathbf{Z}\)는 모든 \(z^{(i)}\)를 포함하는 행렬)

선형적인 지역 관계 모델링은 샘플을 고정하고 최적의 가중치를 찾는 대신, 차원 축소는 반대로 가중치를 고정하고 저차원의 공간에서 샘플 이미지의 최적 위치를 찾는다.

관계를 보존하는 차원 축소

\[\mathbf{Z}=\underset{\mathbf{z}}{argmin}\sum^m_{i=1}(\mathbf{z}^{(i)}-\sum^m_{j=1}\hat{w}_{i,j}\mathbf{z}^{(j)})^2\]

잡음이 너무 많지 않은 경우 꼬인 매니폴드를 펼치는 데 잘 작동
계산 복잡도는 k개의 가까운 이웃을 찾는데 \(O(mlog(m)nlog(k))\), 가중치 최적화에 \(O(mnk^3)\), 저차원 표현을 만드는데 \(O(dm^2)\)
대량의 데이터셋에 적용하기 어렵다(계산 복잡도에서 저차원 표현 만들때 \(m^2\) 때문)

6. 다른 차원 축소 기법

랜덤 투영: 랜덤한 선형 투영을 사용해 데이터를 저차원 공간으로 투영.
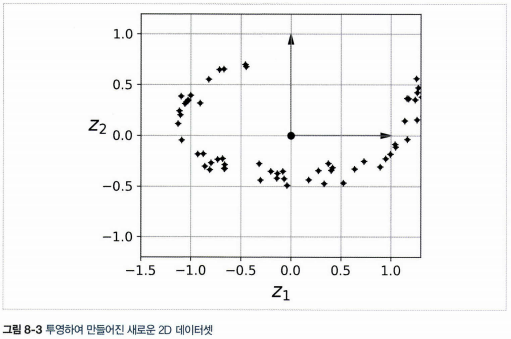
다차원 스케일링(MDS): 샘플 간의 거리를 보존하면서 차원을 축소
Isomap: 각 샘플을 가장 가까운 이웃과 연결하는 식으로 그래프 생성, 그 다음 샘플 간의 지오데식 거리(두 노드 사이의 최단 경로를 이루는 노드의 수)를 유지하면서 차원 축소
t-SNE: 비슷한 샘플은 가까이, 비슷하지 않은 샘플은 멀리 떨어지도록 하면서 차원 축소. 주로 시각화에 사용(고차원 공간에 있는 샘플의 군집을 시각화할 때)
선형 판별 분석(LDA): 원래는 분류 알고리즘이나 훈련 과정에서 클래스 사이를 잘 구분하는 축을 학습. 이 축을 데이터가 투영되는 초평면을 정의하는 데 사용. 투영을 통해 가능한 클래스를 멀리 떨어지게 유지시키므로 SVM 분류기 같은 다른 분류 알고리즘을 적용하기 전에 차원 축소시키는 데 좋다.