서포트 벡터 머신

Published: Jun 1, 2020 by Dev-hwon

이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.

서포트 벡터 머신 (Support Vector Machine, SVM)

선형이나 비선형 분류, 회귀, 이상치 탐색에도 사용할 수 있는 다목적 머신러닝 모델
복잡한 분류 문제에 잘 들어맞으며 작거나 중간 크기의 데이터셋에 적합
확률을 직접 계산하지 않고 데이터가 어떤 ‘경계선’을 넘는지 넘지 않는지 검사하여 분류한다.
종속변수를 두 개 그룹으로 구분하여 중심선을 구하여, 2개 이상의 그룹으로 구분 될 경우에만 각 그룹별로 모두 중심선을 구한 후, 향후 판별시에 여러 중심선을 함께 고려하여 연산한다.
특성의 스케일에 민감하다.

장점	단점
* 구조적이며 매번 수행해도 결과가 어느정도 비슷함 * 경계선 근처의 데이터들만 고려하기 때문에 모델이 가볍고 노이즈에 강함	* 구체적 확률값 구하기 어려움

1. 선형 SVM 분류

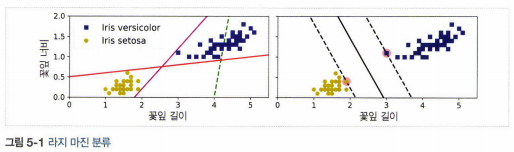
라지 마진 분류: 결정 경계가 클래스를 잘 나누고 제일 가까운 훈련 샘플로부터 가능한 멀리 떨어져 있는 직선일 때

2. 소프트 마진 분류

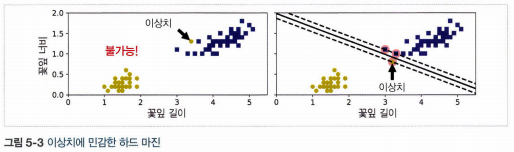
하드 마진 분류: 모든 샘플이 결정 경계 바깥쪽으로 올바르게 분류 되어 있는 경우
하드 마진 분류의 문제점: 데이터가 선형적으로 구분될 수 있어야 제대로 작동하며, 이상치에 민감하다.

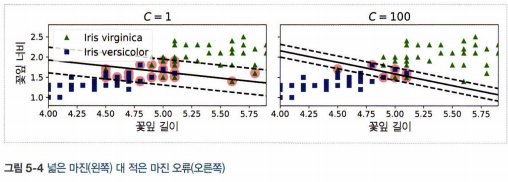
소프트 마진 분류: 도로의 폭을 가능한 넓게 유지하는 것과 마진 오류 사이에 적절한 균형을 잡는 것
하이퍼파라미터 C를 조정. 낮게 설정하면 도로의 폭이 넓어지는 대신 마진 오류가 증가하고, 높게 설정하면 도로의 폭이 좁아지는 대신 마진 오류가 적어진다.
일반적으로 마진 오류가 적은 것이 좋다.

3. 비선형 SVM 분류

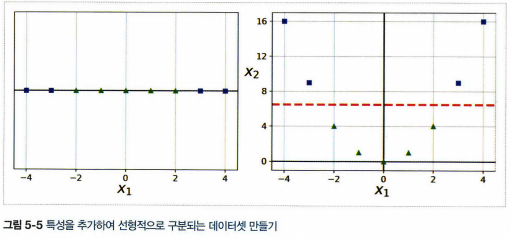
비선형 데이터셋에 다항 특성과 같은 특성을 더 추가하여 선형적으로 구분되는 데이터셋으로 변경
간단하고 모든 머신러닝 알고리즘에서 잘 작동
낮은 차수의 다항식은 매우 복잡한 데이터셋을 잘 표현하지 못하고 높은 차수의 다항식은 많은 특성을 추가하므로 모델을 느리게 만든다.

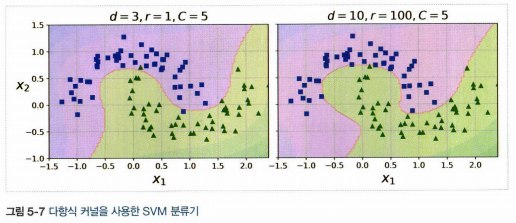
3.1. 다항식 커널

커널 트릭: 실제로 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있다.

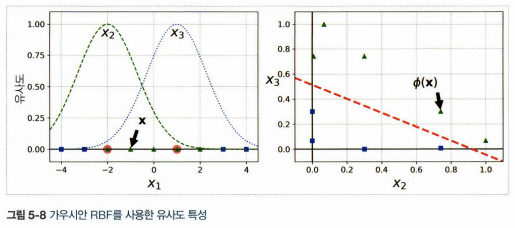
3.2. 유사도 특성

비선형 특성을 다루는 다른 기법으로 각 샘플이 특정 랜드마크와 얼마나 닮았는지 측정하는 유사도 함수로 계산한 특성을 추가하는 것
예:

랜드마크 \(x_1=-2\)와 \(x_1=1\)이라 하고, \(\gamma=0.3\)인 가우시안 방사 기저 함수(RBF)를 유사도 함수라고 정의하는 경우

가우시안 RBF : \(\phi_{\gamma}(\mathbf{x},l)=exp(-\gamma{\Vert \mathbf{x}-l \Vert}^2)\)

\(x_1=-1\)인 샘플의 경우 새로 만들어지는 특성 \(x_2=exp(-0.3\times1^2)\approx 0.74, x_3=exp(-0.3\times2^2)\approx 0.30\)이다.

랜드마크를 설정하는 방법: 데이터셋에 있는 모든 샘플 위치에 랜드마크를 설정하는 것 (차원이 매우 커지고 변환된 훈련 세트가 선형적으로 구분될 가능성이 높다.)
단점: 훈련 세트에 있는 n개의 특성을 가진 m개의 샘플이 m개의 특성을 가진 m개의 샘플로 변환된다는 것, 훈련 세트가 매우 클 경우 동일한 크기의 특성이 만들어진다.

3.3. 가우시안 RBF 커널

유사도 특성을 많이 추가하는 것과 같은 비슷한 결과
gamma를 증가시키면 종 모양 그래프가 좁아져 각 샘플의 영향 범위가 작아진다. 반대로 gamma를 작게하면 넓은 종 모양 그래프를 만들며 샘플이 넓은 범위에 걸쳐 영향을 준다.

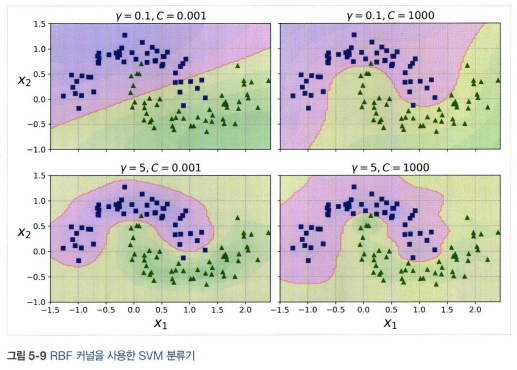
먼저 선형 커널을 시도(특히 훈련 세트가 아주 크거나 특성 수가 많을 경우), 훈련 세트가 너무 크지 않다면 가우시안 RBF 커널 시도

3.4 계산 복잡도

파이썬 클래스	시간 복잡도	외부 메모리 학습 지원	스케일 조정의 필요성	커널 트릭
LinearSVC	\(O(m \times n)\)	아니오	예	아니오
SGDClassifier	\(O(m \times n)\)	예	예	아니오
SVC	\(O(m^2 \times n) \sim O(m^3 \times n)\)	아니오	예	예

4. SVM 회귀

SVM을 분류가 아니라 회귀에 적용하는 방법은 목표를 반대로 하는 것
제한된 마진 오류 안에서 도로 안에 가능한 많은 샘플이 들어가도록 학습

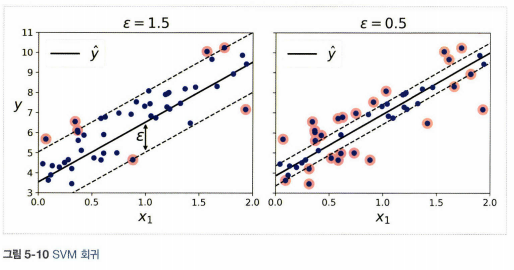
마진 안에서는 훈련 샘플이 추가되어도 모델의 예측에는 영향이 없다. 그래서 이 모델을 \(\varepsilon\)에 민감하지 않다고 말한다.

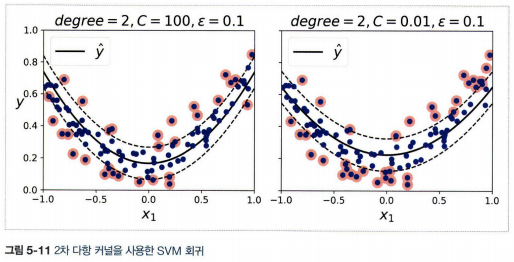
SVR은 SVC의 회귀 버전, LinearSVR은 LinearSVC의 회귀버전

5. SVM 이론

편향을 \(b\)라 하고 특성의 가중치 벡터를 \(\mathbf{w}\), 따라서 입력 특성 벡터에 편향을 위한 특성 추가x

5.1. 결정 함수와 예측

선형 SVM 분류기 모델은 단순히 결정 함수를 계산해서 새로운 샘플 \(\mathbf{x}\)의 클래스를 예측

결정 함수 : \(\mathbf{w}^T\mathbf{x}+b=w_{1}x_{1}+\cdots+w_{n}x_{n}+b\)

결괏값이 0보다 크면 예측된 클래스 \(\hat{y}\)는 양성 클래스(1), 그렇지 않으면 음성 클래스(0)

\[\hat{y}=\left\{\begin{matrix} 0 & \mathbf{w}^T\mathbf{x}+b < 0일 때 \\ 1 & \mathbf{w}^T\mathbf{x}+b \geq 0일 때 \end{matrix}\right.\]

결정 경계는 결정 함수의 값이 0인 점들로 이루어져 있으며, 특성이 두개인 데이터에서는 데이터셋의 2차원 평면, 결정 함수를 나타내는 평면, 두 평면의 교차점으로 직선이다.
점선은 결정 함수의 값이 1 또는 -1인 점들을 나타낸다.

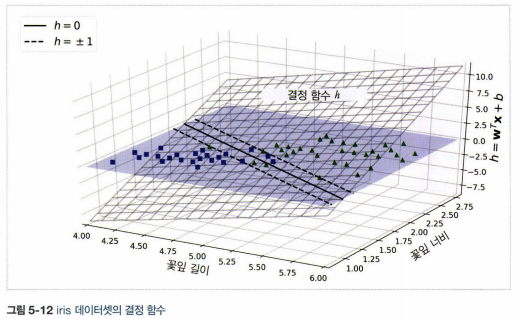
5.2. 목적함수

가중치 벡터 \(\mathbf{w}\)가 작을수록 마진은 커진다.
마진을 크게 하기 위해 \(\Vert \mathbf{w} \Vert\)를 최소화

하드 마진 선형 SVM 분류기의 목적함수 :

\[\underset{w,b}{minimize} \frac{1}{2}\mathbf{w}^T\mathbf{w}\] \[[조건] i=1,2,\cdots,m일 때\] \[t^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)\geq 1\]

\(\Vert \mathbf{w} \Vert\)는 \(\mathbf{w}=0\)에서 미분할 수 없으므로 \(\frac{1}{2}{\Vert \mathbf{w} \Vert}^2\)인 \(\frac{1}{2} \mathbf{w}^{T}\mathbf{w}\)를 최소화
소프트 마진 분류기의 경우 각 샘플에 대해 슬랙 변수 \(\zeta^{(i)} \geq 0\)을 도입(\(\zeta^{(i)}\))는 i번째 샘플이 얼마나 마진을 위반할지 정함)
마진 오류를 최소화하기 위해 슬랙 변수의 값을 작게 만드는 것과 마진을 크게 하기 위해 \(\frac{1}{2} \mathbf{w}^{T}\mathbf{w}\)를 작게 만드는 것이 상충된다.
하이퍼파라미터 C는 두 목표 사이의 트레이드오프를 정의

소프트 마진 선형 SVM 분류기의 목적함수 :

\[\underset{w,b,\zeta}{minimize} \frac{1}{2}\mathbf{w}^T\mathbf{w}+C\sum^m_{i=1}\zeta^{(i)}\] \[[조건] i=1,2,\cdots,m일 때\] \[t^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)\geq 1-\zeta^{(i)} 이고 \zeta^{(i)} \geq 0\]

5.3 콰드라틱 프로그래밍

선형적인 제약 조건이 있는 볼록 함수의 이차 최적화 문제를 콰드라틱 프로그래밍(QP) 문제라고 한다.

QP 문제 :

\[\underset{\mathbf{p}}{minimize} \frac{1}{2}\mathbf{p}^T\mathbf{H}\mathbf{p}+\mathbf{f}^{T}\mathbf{p}\] \[[조건] \mathbf{Ap} \leq \mathbf{b}\] \[여기서 \left\{\begin{matrix} \mathbf{p}는 n_p차원의 벡터(n_p = 모델 파라미터 수)\\ \mathbf{H}는 n_p \times n_p 크기 행렬\\ \mathbf{f}는 n_p차원의 벡터\\ \mathbf{A}는 n_c \times n_p 크기 행렬 (n_c = 제약수)\\ \mathbf{b}는 n_c차원의 벡터 \end{matrix}\right.\]

다음과 같이 QP 파라미터를 지정하면 하드 마진을 갖는 선형 SVM 분류기의 목적 함수를 간단하게 검증 가능

\(n_p=n+1\), 여기서 \(n\)은 특성 수 (편향 때문에 +1)

\(n_c=m\),여기서 \(m\)은 룬련 샘플 수

\(\mathbf{H}\)는 \(n_p \times n_p\) 크기이고 왼쪽 맨 위의 원소가 0(편향을 제외하기 위해)인 것을 제외하고는 단위행렬

\(\mathbf{f}=0\), 모두 0으로 채워진 \(n_p\)차원의 벡터

\(\mathbf{b}=1\), 모두 1로 채워진 \(n_c\)라원의 벡터

\(a^{(i)}=-t^{(i)}\dot{\mathbf{x}}^{(i)}\), 여기서 \(\dot{\mathbf{x}}^{(i)}\)는 편향을 위해 특성 \(\dot{\mathbf{x}}_0=1\)을 추가한 \(\mathbf{x}^{(i)}\)와 같다.

5.4 쌍대문제

쌍대이론: 모든 선형계획 문제는 원문제와 쌍대문제로 작성 될 수 있고, 분석될 수 있음을 말함. 원문제는 그와 짝을 이루는 쌍대문제로 변형이 가능하고, 두 문제간의 관계는 매우 긴밀함

선형 SVM 목적 함수의 쌍대 형식

\[\underset{\alpha}{minimize}\frac{1}{2}\sum^m_{i=1}\sum^m_{j=1}\alpha^{(i)}\alpha^{(j)}t^{(i)}t^{(j)}\mathbf{x}^{(i)^T}\mathbf{x}^{(j)}-\sum^m_{i=1}\alpha^{(i)}\]

쌍대 문제에서 구한 해로 원 문제의 해 계산하기

\[\hat{\mathbf{w}}=\sum^m_{i=1}\hat{\alpha}^{(i)}t^{(i)}\mathbf{x}^{(i)}\] \[\hat{b}=\frac{1}{n_s}\underset{\hat{\alpha}^{(i)}>0}{\sum^m_{i=1}}(t^{(i)}-\hat{w}^{T}\mathbf{x}^{(i)})\]

훈련 샘플 수가 특성 개수보다 작을 때 원문제보다 쌍대 문제를 푸는 것이 더 빠르다.
원문제에서 적용이 안되는 커널 트릭을 가능하게 한다.

5.5 커널 SVM

변환을 계산하지 않고 원래 벡터 \(a\)와 \(b\)에 기반하여 계산할 수 있게 하는 함수
예: 2차 다항식 커널

2차원 데이터셋에 2차 다항식 변환 적용(2차 다항식 매핑 함수 \(\phi\))

\[\phi(\mathbf{x})=\phi\begin{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix}\end{pmatrix} = \begin{pmatrix} x_1^2\\ \sqrt{2}{x_1}{x_2}\\ x_2^2 \end{pmatrix}\]

2차 다항식 매핑을 위한 커널 트릭

\[\phi(\mathbf{a})^{T}\phi(\mathbf{b}) = \begin{pmatrix} a_1^2\\ \sqrt{2}{a_1}{a_2}\\ a_2^2 \end{pmatrix}^2 \begin{pmatrix} b_1^2\\ \sqrt{2}{b_1}{b_2}\\ b_2^2 \end{pmatrix} = a_1^{2}b_1^{2}+2a_1b_1a_2b_2+a_2^{2}b_2^{2} = (a_1b_1+a_2b_2)^2 = \begin{pmatrix} \begin{pmatrix} a_1\\ a_2 \end{pmatrix}^T & \begin{pmatrix} b_1\\ b_2 \end{pmatrix} \end{pmatrix}^2 = (\mathbf{a}^T\mathbf{b})^2\]

변환된 벡터의 점곱이 원래 벡터의 점곱의 제곱과 같다. \(\phi(\mathbf{a})^{T}\phi(\mathbf{b}) = (\mathbf{a}^T\mathbf{b})^2\)

일반적인 커널

선형: \(K(\mathbf{a},\mathbf{b})=\mathbf{a}^T\mathbf{b}\)

다항식: \(K(\mathbf{a},\mathbf{b})=(\gamma\mathbf{a}^T\mathbf{b}+r)^d\)

가우시안 RBF: \(K(\mathbf{a},\mathbf{b})=exp(-\gamma\Vert a-b \Vert^2)\)

시그모이드: \(K(\mathbf{a},\mathbf{b})=tanh(\gamma\mathbf{a}^T\mathbf{b}+r)\)

머서의 정리: 함수 \(K(\mathbf{a},\mathbf{b})\)가 머서의 조건(\(K(\mathbf{a},\mathbf{b})=K(\mathbf{b},\mathbf{a})\) 등)이라 부르는 몇 개 수학적 조건을 만족할 때 \(\mathbf{a}\)와\(\mathbf{b}\)를 다른 공간에 매핑하는 함수 \(\phi\)가 존재
쌍대 문제를 풀어서 원문제를 해결하는 방법

\(\hat{\mathbf{w}}\)에 대한 식을 새로운 샘플 \(\mathbf{x}^{(n)}\)의 결정 함수에 적용해서 입력 벡터 간의 점곱으로만 된 식을 얻을 수 있고, 커널 트릭을 사용할 수 있게 된다.

커널 SVM으로 예측하기

\[h_{\hat{\mathbf{w}}\hat{b}}(\phi(\mathbf{x}^{(n)}))=\hat{\mathbf{w}}^{T}\phi(\mathbf{x}^{(n)})+\hat{b}=(\sum^m_{i=1}\hat{\alpha}^{(i)}t^{(i)}\phi(\mathbf{x}^{(i)}))^{T}\phi(\mathbf{x}^{(n)})+\hat{b} \\ = \sum^m_{i=1}\hat{\alpha}^{(i)}t^{(i)}(\phi(\mathbf{x}^{(i)})^T\phi(\mathbf{x}^{(n)}))+\hat{b} \\ = \underset{\hat{\alpha}^{(i)}>0}{\sum^m_{i=1}}\hat{\alpha}^{(i)}t^{(i)}K(\mathbf{x}^{(i)}, \mathbf{x}^{(n)})+\hat(b)\]

서포트 벡터만 \(\alpha^{(i)} \neq 0\)이기 때문에 예측을 만드는 데는 전체 샘플이 아니라 서포트 벡터와 새 입력 벡터 \(\mathbf{x}^{(n)}\)간의 점곱만 계산하면 되며 편향 \(\hat{b}\)도 커널 트릭을 사용해 계산해야한다.

커널 트릭을 사용한 편향 계산

\[\hat{b}=\frac{1}{n_s}\underset{\hat{\alpha}^{(i)}>0}{\sum^m_{i=1}}(t^{(i)}-\hat{\mathbf{w}^T\phi(\mathbf{x}^{(i)})})=\frac{1}{n_s}\underset{\hat{\alpha}^{(i)}>0}{\sum^m_{i=1}}(t^{(i)}-(\sum^m_{j=1}\hat{\alpha}^{(j)}t^{(j)}\phi(\mathbf{x}^{(j)}))^{T}\phi(\mathbf{x}^{(i)})) \\ = \frac{1}{n_s}\underset{\hat{\alpha}^{(i)}>0}{\sum^m_{i=1}}(t^{(i)}-\underset{\hat{\alpha}^{(j)}>0}{\sum^m_{j=1}}\hat{\alpha}^{(j)}t^{(j)}K(\mathbf{x}^{(i)}, \mathbf{x}^{(j)}))\]

5.6 온라인 SVM

원 문제로 부터 유도된 비용 함수를 최소화하기 위한 경사 하강법을 사용
경사 하강법은 QP 기반의 방법보다 훨씬 느리게 수렴

선형 SVM 분류기 비용 함수

\[J(\mathbf{w},b)=\frac{1}{2}\mathbf{w}^{T}\mathbf{w}+C\sum^m_{i=1}max(0,1-t^{(i)})(\mathbf{w}^{T}\mathbf{x}^{(i)}+b)\]

힌지 손실: \(max(0,1-t)\)함수를 힌지 손실 함수라고 부른다.