Published: Jun 1, 2020 by Dev-hwon
이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.
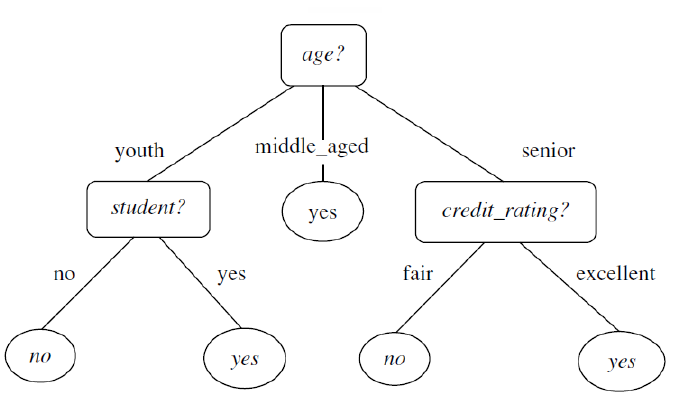
의사 결정 나무(결정 트리, Decision Tree)
- 스무고개와 비슷하게 일련의 질문들을 통해 의사결정 규칙을 나무 구조로 도식화하여 분류와 예측을 모두 수행할 수 있는 분석 방법
- 복잡한 데이터셋도 학습 가능
| 장점 | 단점 |
|---|---|
| * 연속형과 명목형 모두 처리 가능 * 비선형, 불연속 데이터도 학습 가능 * 계산 속도가 빠름 * 결과 해석이 비교적 쉬움 * 데이터 전처리가 거의 필요하지 않다. |
* 데이터의 작은 변화에도 구조가 민감하게 변화 * 트리가 커질수록 과적합에 빠질 수 있음 * Missing value 처리 불가능 |
1. 예측
- 루트 노트(깊이가 0인 맨 꼭대기의 노드)에서 시작하여 조건에 맞는 자식 노드로 이동. 자식 노드가 리프 노드(자식을 가지지 않는 노드)일 경우 추가 검사를 하지 않는다.
2. 클래스 확률 추정
- 샘플에 대해 리프 노드를 찾기 위해 트리를 탐색하고 그 노드에 있는 클래스 k의 훈련 샘플의 비율을 반환
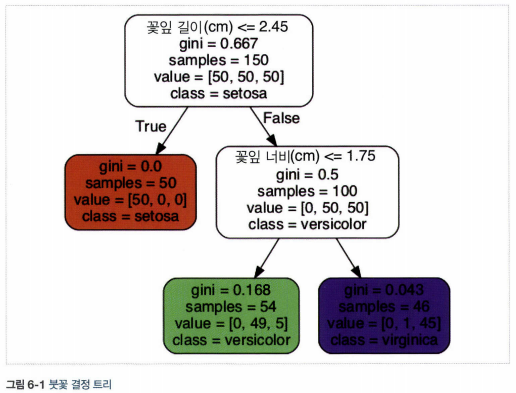
- ex) 길이가 5cm, 너비가 1.5cm 꽃잎은 리프 노드의 깊이 2에서 왼쪽 노드이고, Setosa는 0%(0/54), Versicolor는 90.7%(49/54), Virginica는 9.3%(5/54)
3. CART 훈련 알고리즘
- 사이킷런은 결정 트리를 훈련시키기 위해 CART 알고리즘 사용
- 훈련 세트를 하나의 특성 \(k\)의 임곗값 \(t_k\)를 사용해 가장 순수한 서브셋으로 나눌 수 있는 두개의 서브셋을 나눈다. 이 과정을 반복한다.
- 최대 깊이가 되면 중지하거나 불순도를 줄이는 분할을 찾을 수 없을 때 중지
분류에 대한 CART 비용 함수
\[J(k,t_k)=\frac{m_{left}}{m}G_{left}+\frac{m_{right}}{m}G_{right}\] \[여기서 \left\{\begin{matrix} G_{left/right}는 왼쪽/오른쪽 서브넷의 불순도\\ m_{left/right}는 왼쪽/오른쪽 서브넷의 샘플 수 \end{matrix}\right.\]4. 계산 복잡도
- 각 노드는 하나의 특성값만 확인하기 때문에 예측에 필요한 전체 복잡도는 특성 수와 무관하게 \(O({log}_2(m))\)
- 훈련 알고리즘은 각 노드에서 모든 훈련 샘플의 모든 특성을 비교. 훈련 복잡도는 \(O(n \times mlog(m))\)
5. 지니 불순도와 엔트로피
- 기본적으로 지니 불순도를 사용하지만 critertion 매개변수를 “entropy”로 지정하며 엔트로피 불순도를 사용할 수 있다.
- 지니 불순도가 조금 더 계산이 빠르기 때문에 기본값으로 사용
- 지니 불순도와 엔트로피가 서로 다른 트리가 만들어지는 경우 지니 불순도가 가장 빈도 높은 클래스를 한쪽 가지로 고립시키는 경향이 있고, 엔트로피는 조금 더 균형 잡힌 트리를 만든다.
지니 불순도
\[G_i=1-\sum^n_{k=1}P_{i,k}^2\]\(P_{i,k}\)는 i번째 노드에 있는 훈련 샘플 중 클래스 k에 속한 샘플의 비율
엔트로피 불순도
\[H_i=-\underset{P_{i,k} \neq 0}{\sum^n_{k=1}}log_2(P_{i,k})\]6. 규제 매개변수
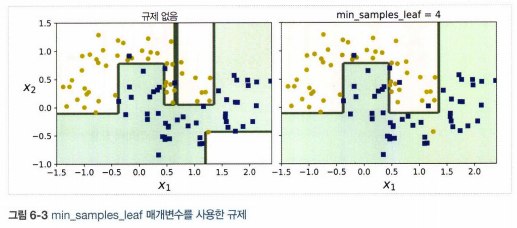
- 제한을 두지 않으면 트리가 훈련 데이터에 과대적합되기 쉽다.
- 결정트리는 훈련되기 전에 파라미터 수가 결정되지 않기 때문에 비파라미터 모델이라고 부른다.
- 모델 구조가 데이터에 맞춰져서 고정되지 않고 자유롭다.
- max_depth, min_samples_split, min_samples_leaf, min_weight_fraction_leaf, max_leaf_nodes, max_features
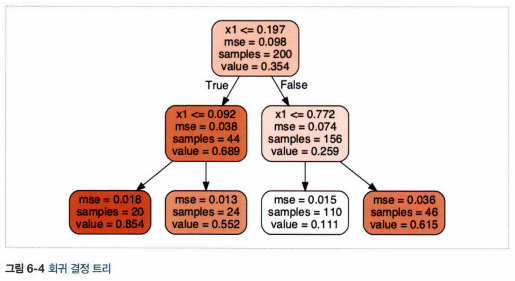
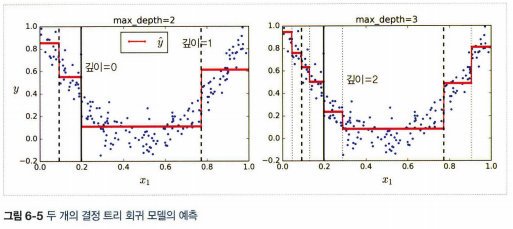
7. 회귀
- 사이킷런의 DecisionTreeRegressor 사용
- 각 영역의 예측값은 항상 그 영역에 있는 타깃값의 평균
- 예측값과 가능한 많은 샘플이 가까이 있도록 영역 분할
회귀를 위한 CART 비용 함수
\[J(k,t_k)=\frac{m_{left}}{m}{MSE}_{left}+\frac{m_{right}}{m}{MSE}_{right}\] \[여기서 \left\{\begin{matrix} {MSE}_{node} = \sum_{i \in node}(\hat{y}_{node}-y^{(i)})^2\\ \hat{y}_{node} = \frac{1}{m_{node}}\sum_{i \in node}y^{(i)} \end{matrix}\right.\]8. 불안정성
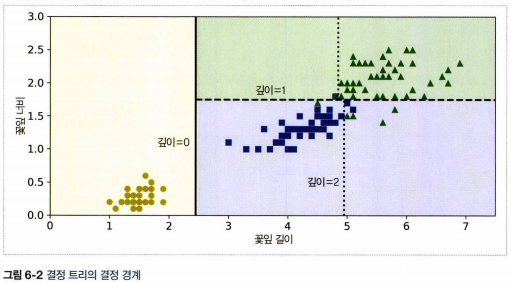
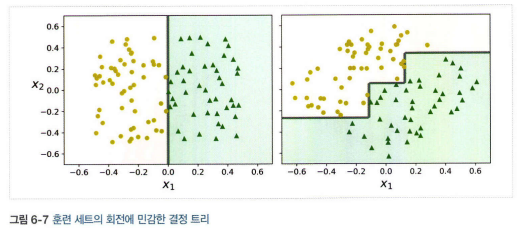
- 결정 트리는 계단 모양의 결정 경계를 만들기 때문에 훈련 세트의 회전에 민감하다.(PCA기법을 이용하여 더 좋은 방향으로 회전시키는 방법 이용)
- 훈련 데이터에 있는 작은 변화에도 매우 민감하다.