Published: May 28, 2020 by Dev-hwon
이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.
목차
규제 (Regulation)
- 과대적합을 감소시키는 방법
- 선형 회귀 모델에서는 모델의 가중치를 제한함으로써 규제
- ‘릿지’, ‘라쏘’, ‘엘라스틱넷’
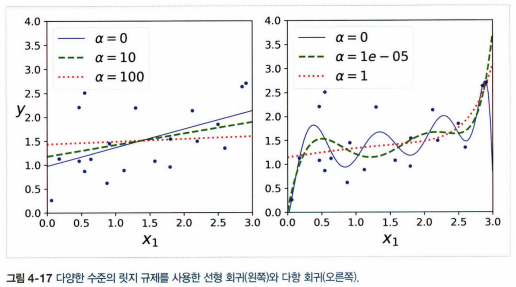
1. 릿지 회귀(또는 티호노프 규제)
- 규제항 \(\alpha\sum^{n}_{i=1}\theta^2_i\)이 비용 함수에 추가
- 학습 알고리즘을 데이터에 맞추는 것뿐만 아니라 모델의 가중치가 가능한 작게 유지되도록 한다.
- 모델의 훈련이 끝나면 모델의 성능을 규제가 없는 성능 지표로 평가
- \(\alpha=0\)이면 릿지 회귀는 선형회귀와 같아지고, \(\alpha\)가 아주 크면 모든 가중치가 0에 가까워지고 데이터의 평균을 지나는 수평선이 된다.
- 릿지 회귀의 비용 함수: \(J(\theta)=MSE(\theta)+\alpha\frac{1}{2}\sum^{m}_{i=1}\theta^2_i\)
- 릿지 회귀의 정규방정식: \(\hat{\theta}=(\mathbf{X}^{T}\mathbf{X}+\alpha{A})^{-1}\mathbf{X}^{T}\mathbf{y}\)
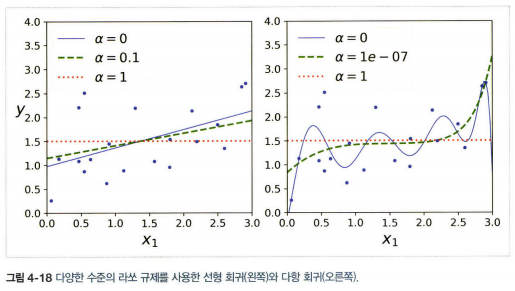
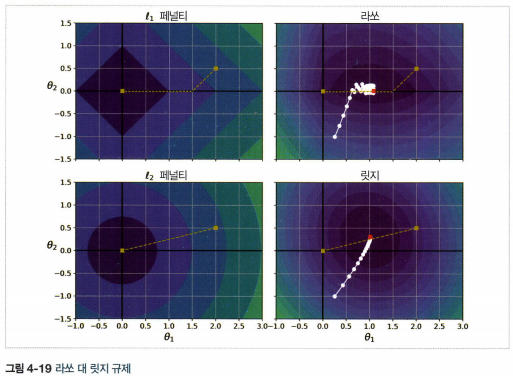
2. 라쏘 회귀
- 릿지 회귀처럼 비용 함수에 규제항을 더하지만 \(\mathit{l}_2\) 노름의 제곱을 2로 나눈 것 대신 가중치 벡터 \(\mathit{l}_1\) 노름을 사용한다.
- 덜 중요한 특성의 가중치를 제거하려 한다는 특징
- 라쏘 회귀 비용 함수: \(J(\theta)=MSE(\theta)+\alpha\sum^{n}_{i=1} \vert {\theta_i} \vert\)
- 라쏘의 비용 함수는 \(\theta_i = 0 (i=1,2,\cdots,n일 때)\)에서 미분 불가능, 하지만 \(\theta_i = 0\)일 때 서브그레디언트 벡터 \(\mathbf{g}\)를 사용하면 경사 하강법 적용 가능
- 라쏘 회귀의 서브그레디언트 벡터
\(\mathbf{g}(\theta,J)=\triangledown_{\theta}MSE+\alpha\begin{pmatrix} \mathrm{sign}(\theta_1) \\ \mathrm{sign}(\theta_2) \\ \vdots \\ \mathrm{sign}(\theta_n) \end{pmatrix}\) 여기서 \(\mathrm{sign}(\theta_i)= \left \{\begin{matrix} -1& \theta_i < 0일 때 \\ 0& \theta_i = 0일 때 \\ +1& \theta_i > 0일 때 \end{matrix} \right.\)
3. 엘라스틱넷
- 릿지 회귀와 라쏘 회귀를 절충한 모델
- 릿지와 라쏘의 규제항을 더해서 사용, 혼합 비율 \(r\)을 사용해 조절
- \(r=0\)이면 릿지 회귀, \(r=1\)이면 라쏘 회귀와 같다.
- 엘라스틱넷 비용 함수: \(J(\theta)=MSE(\theta)+r\alpha\sum^{n}_{i=1} \vert {\theta_i} \vert + \frac{1-r}{2}\alpha\sum^n_{i=1}\theta_i^2\)
- 릿지를 기본을 사용, 쓰이는 특성이 몇 개뿐이라고 의심되면 라쏘나 엘라스틱넷 사용, 특성 수가 훈련 샘플 수보다 많거나 특성 몇 개가 강하게 연관되어 있을 때는 라쏘보다는 엘라스틱넷 선호
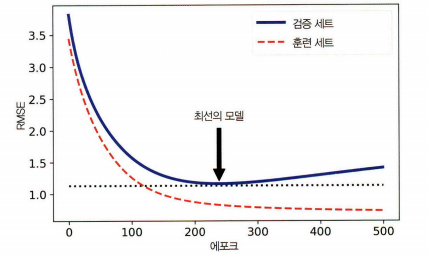
4. 조기종료
- 검증 에러가 최솟값에 도달하면 바로 훈련을 중지시키는 것