Published: May 28, 2020 by Dev-hwon
이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.
목차
경사 하강법 (Gradient Desent, GR)
- 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반 적인 최적화 알고리즘
- 비용 함수를 최소화하기 위해 반복해서 파라미터를 조정해가는 방법
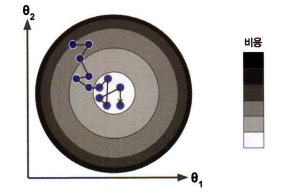
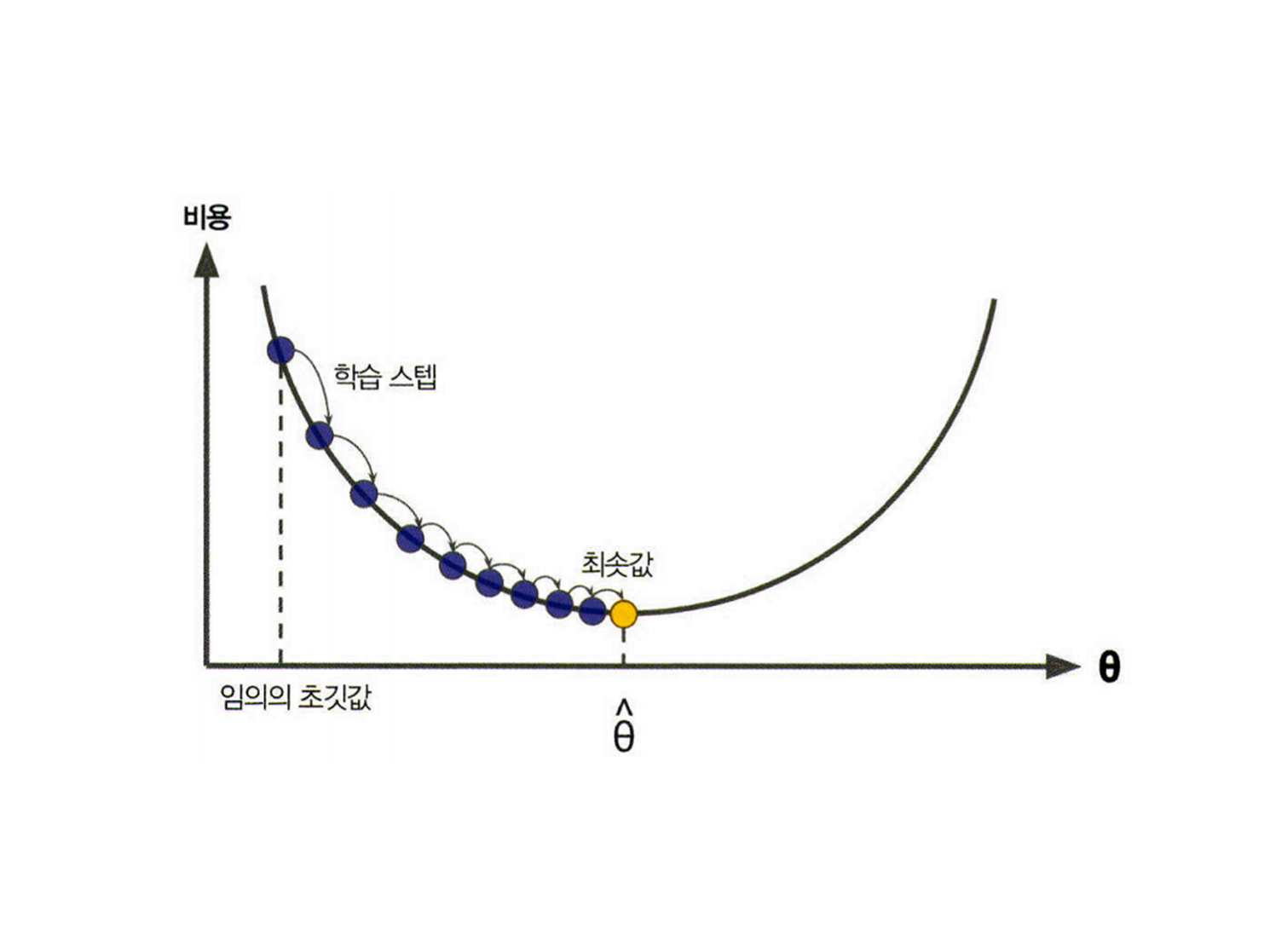
파라미터 벡터 \(\theta\)를 임의의 값으로 시작해서(무작위 초기화) 비용 함수의 현재 그래디언트를 계산하고, 그래디언트가 감소하는 방향으로 진행하여 알고리즘이 최솟값에 수렴할 때까지 점진적으로 향상
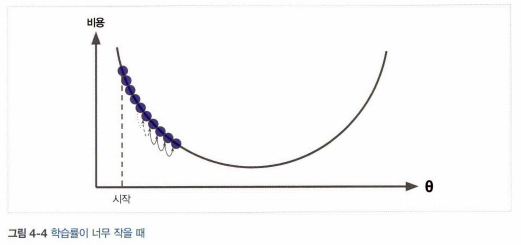
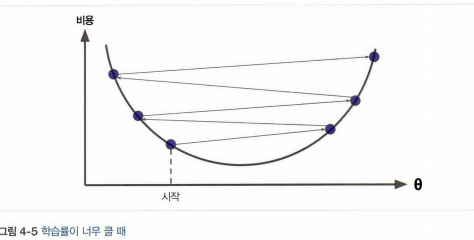
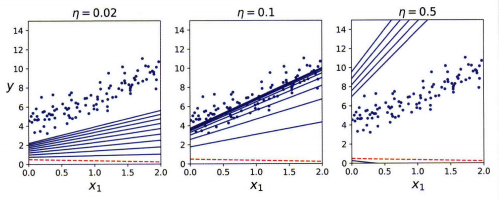
- 학습률(learning late): 경사 하강법에서 중요한 파라미터로 스텝의 크기를 나타낸다. 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 진행해야 하므로 시간이 오래 걸리고, 학습률이 너무 크면 골짜기를 가로질러 반대편으로 건너뛰게 되어 이전보다 더 큰값으로 발산하게 만들 수 있다.
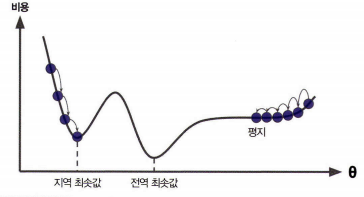
- 경사 하강법의 문제점:
1) 전역 최솟값보다 지역 최솟값에 수렴할 수 있다.
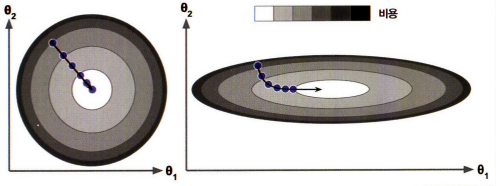
2) 특성들의 스케일이 다르면 최솟값에 도달하는데 시간이 오래 걸린다.
1. 배치 경사 하강법
- 매 경사 하강법 스텝에서 전체 훈련 세트 \(\mathbf{x}\)에 대해 계산하는 방법
- 매우 큰 훈련 세트에서는 아주 느리다.
- 특성 수에 민감하지 않다.
- 편도함수: 각 모델 파라미터 \(\theta_{j}\)가 조금 변경 될 때 비용함수가 얼마나 바뀌는지 계산하는 함수
- 그레디언트 벡터
- 경사 하강법의 스텝: \({\theta}^{(\mathrm{nextstep})}={\theta}-{\eta}{\triangledown_{\theta}}{MSE}(\theta)\)
2. 확률적 경사 하강법
- 매 스텝에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 그레디언트 계산하는 방법
- 매 반복에서 다뤄야 할 데이터가 적기 때문에 빠르고 매우 큰 훈련 세트도 가능하다.
- 비용 함수가 매우 불규칙할 경우 지역 최솟값을 건너뛸 수 있도록 도와주므로 배치 경사 하강법보다 전역 최솟값을 찾을 가능성이 높다.
- 반면에 확률적이기 때문에 배치 경사 하강법보다 불안정하여 전역 최솟값에 다다르지 못하게 한다.
- 해결법: 학습률을 점진적으로 감소시킨다.
- 학습 스케줄: 매 반복에서 학습률을 결정하는 함수
3. 미니배치 경사 하강법
- 미니배치라 부르는 임의의 작은 샘플 세트에 대해 그레디언트를 계산
- 행렬 연산에 최적화된 하드웨어, 특히 GPU를 사용해서 얻는 성능 향상
- SGD보다 최솟값에 더 가까이 도달할 수 있다.
- 하지만 지역 최솟값에서 더 빠져나오기 힘들 수 있다.
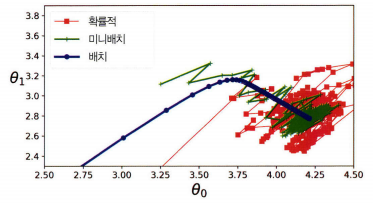
- 배치 경사 하강법의 경로가 실제로 최솟값에서 멈춘 반면 확률적 경사 하강법과 미니배치 경사 하강법은 근처에서 맴돌고 있다.
- 배치 경사 하강법은 매 스텝에서 많은 시간이 소요되고, 확률적 경사 하강법과 미니배치 경사 하강법조 적절한 학습 스케줄을 사용하면 최솟값에 도달한다.
4. 선형 회귀를 사용한 알고리즘 비교
| 알고리즘 | m이 클 때 | 외부 메모리 학습 지원 | n이 클 때 | 하이퍼파라미터 수 | 스케일 조정 필요 | 사이킷런 |
|---|---|---|---|---|---|---|
| 정규방정식 | 빠름 | No | 느림 | 0 | No | N/A |
| SVD | 빠름 | No | 느림 | 0 | No | LinearRegression |
| 배치 경사 하강법 | 느림 | No | 빠름 | 2 | Yes | SGDRegressor |
| 확률적 경사 하강법 | 빠름 | Yes | 빠름 | \(\geq\)2 | Yes | SGDRegressor |
| 미니배치 경사 하강법 | 빠름 | Yes | 빠름 | \(\geq\)2 | Yes | SGDRegressor |