Published: Jul 15, 2020 by Dev-hwon
이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.
고속 옵티마이저
경사 하강법 관련 내용은 Machine Learning 카테고리의 경사 하강법 포스트를 참고하시기 바랍니다. 포스트 보러가기
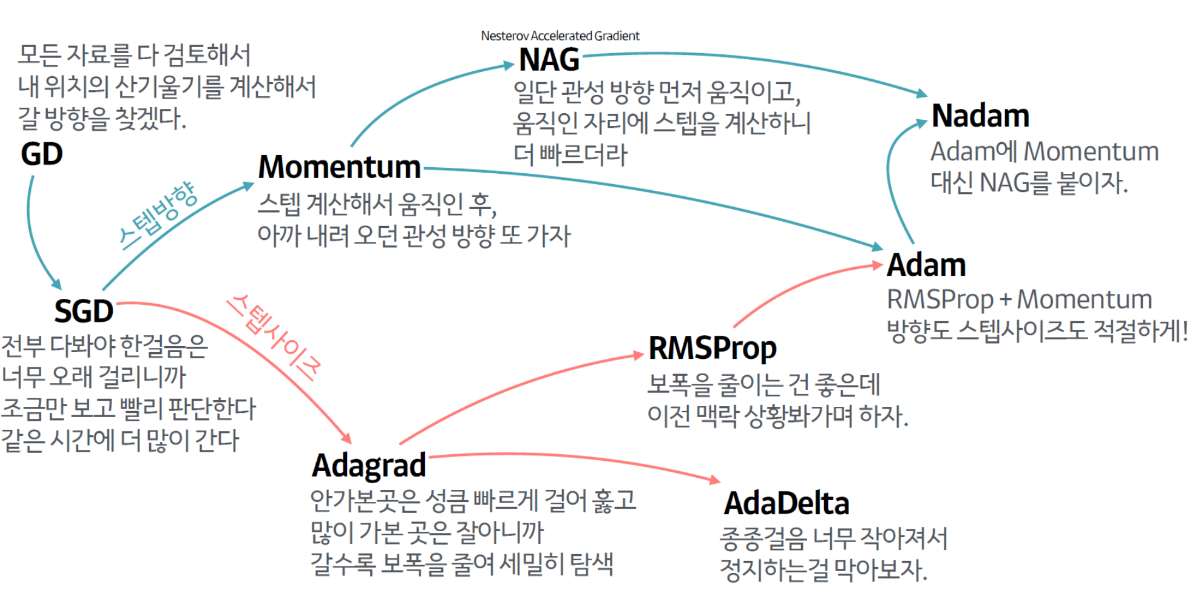
출처: 하용호. 자습해도 모르겠던 딥러닝, 머리속에 인스톨 시켜드립니다. (https://www.slideshare.net/yongho/ss-79607172)
1. 모멘텀 최적화 (Momentum Optimizer)
- 표준적인 경사 하강법은 경사면을 따라 일정한 크기의 스텝으로 조금씩 내려가는 반면 모멘텀 최적화는 처음에는 느리게 출발하지만 종단속도에 도달할 때가지는 빠르게 가속
경사 하강법
\[\theta \leftarrow - \eta{\bigtriangledown} _ \theta J(\theta)\]
모멘텀 알고리즘
- \[\mathbf{m} \leftarrow \beta \mathbf{m} - \eta{\bigtriangledown} _ \theta J(\theta)\]
- \[\theta \leftarrow \theta + \mathbf{m}\]
- 모멘텀 최적화는 이전 그래디언트가 얼마였는지가 상당히 중요
- 현재 그래디언트를 (학습률 \(\eta\)를 곱한 후) 모멘텀 벡터 \(\mathbf{m}\)에 더하고 이 값을 빼는 방식으로 가중치를 갱신
- 일종의 마찰저항을 표현하고 모멘텀이 너무 커지는 것을 막기 위해 모멘텀이라는 새로운 하이퍼파라미터 \(\beta\) 사용(일반적인 모멘텀 값은 0.9)
- 더 바르게 평편한 지역을 탈출하게 도움
- 경사 하강법이 가파른 경사를 꽤 빠르게 내려가지만 좁고 긴 골짜기에서는 오랜 시간이 걸린다. 모멘텀 최적화는 골짜기를 따라 바닥(최적점)에 도달할 때가지 점점 더 빠르게 내려간다.
- 배치 정규화를 사용하지 않는 심층 신경망에서 상위층은 종종 스케일이 매우 다른 입력을 받게 되는데 이런 경우 사용하면 도움이 된다.
- 또한 지역 최적점을 건너뛰도록 하는 데도 도움
optimizer = keras.optimizer.SGD(lr=0.001, momentum=0.9)
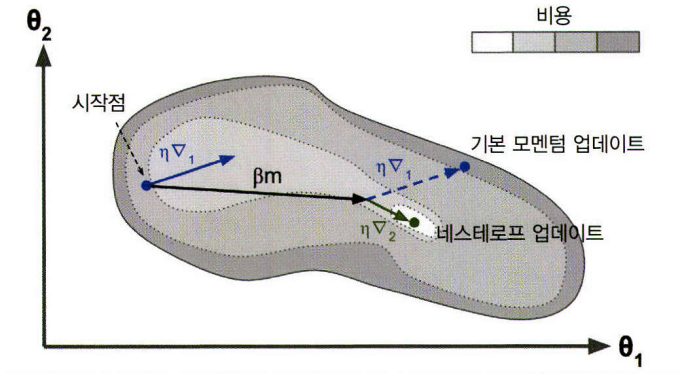
2. 네스테로프 가속 경사 (Nesterov Accelerated Gradient, NAG)
- 현재 위치가 \(\theta\)가 아니라 모멘텀 방향으로 조금 앞선 \(\theta_\beta\mathbf{m}\)에서 비용 함수의 그래디언트를 계산하는 것
네스테로프 가속 경사 알고리즘
- \[\mathbf{m} \leftarrow \beta\mathbf{m}-\eta\bigtriangledown_\theta J(\theta+\beta\mathbf{m})\]
- \[\theta \leftarrow \theta + \mathbf{m}\]
- 원래 위치에서의 그래디언트를 사용하는 것보다 그 방향으로 조금 더 나아가서 측정한 그래디언트를 사용하는 것이 더 정확할 것
- 진동을 감소시키고 수렴을 빠르게 만들어 준다.
- 일반적으로 기본 모멘텀 최적화보다 훈련 속도가 빠르다.
optimizer = keras.optimizer.SGD(lr=0.001, momentum=0.9, nesterov=True)
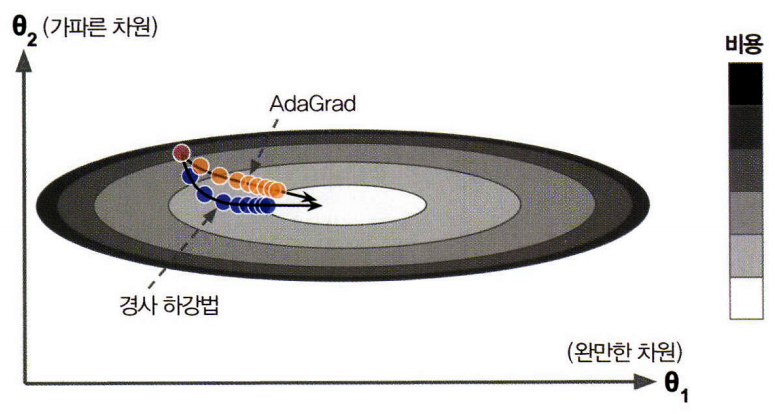
3. AdaGrad
- 가장 가파른 차원을 따라 그래디언트 벡터의 스케일을 감소
AdaGrad 알고리즘
- \[\mathbf{s} \leftarrow \mathbf{s}+\bigtriangledown_\theta J(\theta)\otimes\bigtriangledown_\theta J(\theta)\]
- \[\theta \leftarrow \theta-\eta\bigtriangledown_\theta J(\theta)\oslash \sqrt{\mathbf{s}+\varepsilon}\]
- 첫 번째 단계로 그래디언트 제곱을 벡터 \(\mathbf{s}\)에 누적(각 원소 \(s_i\)마다 파라미터 \(\theta_i\)에 대한 비용 함수의 편미분을 제곱하여 누적)
- 두 번째 단계로 그래디언트 벡터를 \(\sqrt{\mathbf{s}+\varepsilon}\)으로 나누어 스케일을 조정 (\(\oslash\) 기호는 원소별 나눗셈을 나타내고 \(\varepsilon\)은 0으로 나누는 것을 막기 위한 값으로, 일반적으로 \(10^{-10}\))
- 이 알고리즘은 학습률을 감소시키지만 경사가 완만한 차원보다 가파른 차원에 대해 더 빠르게 감소하며 이를 적응적 학습률(adaptive learning)이라고 부르며, 전역 최적점 방향으로 더 곧장 가도록 갱신되는 데 도움
- 학습률 하이퍼파라미터 \(\eta\)를 덜 튜닝해도 되는 점이 또 하나의 장점
- 간단한 2차 방정식 문제에 대해서는 잘 작동하지만 신경망을 훈련할 때 너무 일직 멈추는 경우가 있음. 학습률이 너무 감소되어 전역 최적점에 도착하기전에 알고리즘이 멈춤.
- 케라스에 Adagrad 옵티마이저가 있지만 심층 신경망에 사용하지 말 것
4. RMSProp
- 가장 최근 반복에서 비롯된 그래디언트만 누적함으로써 AdaGrad가 전역 최적점에 도착하기 전에 알고리즘이 멈추는 문제를 해결
- 지수 감소를 사용
RMSProp 알고리즘
- \[\mathbf{s} \leftarrow \beta\mathbf{s}+(1-\beta)\bigtriangledown_\theta J(\theta)\otimes\bigtriangledown_\theta J(\theta)\]
- \[\theta \leftarrow \theta-\eta\bigtriangledown_\theta J(\theta)\oslash \sqrt{\mathbf{s}+\varepsilon}\]
- 보통 감쇠율 \(\beta\)는 0.9로 설정
- 기본값이 잘 작동하는 경우가 많으므로 튜닝할 필요는 전혀 없음
optimizer = keras.optimizer.RMSprop(lr=0.001, rho=0.9)
- rho 매겨변수는 \(\beta\)
- AdaGrad보다 훨씬 더 성능이 좋다.
5. Adam
- 적응적 모멘트 추정(adaptive moment estimation)을 의미
- 모멘텀 최적화와 RMSProp의 아이디어를 합친 것
- 모멘텀 최적화처럼 지난 그래디언트의 지수 감소 평균을 따르고 RMSProp처럼 지난 그래디언트 제곱의 지수 감소된 평균을 따른다.
Adam 알고리즘
- \[\mathbf{m} \leftarrow \beta_1\mathbf{m}-(1-\beta_1)\bigtriangledown_\theta J(\theta)\]
- \[\mathbf{s} \leftarrow \beta_2\mathbf{s}+(1-\beta_2)\bigtriangledown_\theta J(\theta)\otimes\bigtriangledown_\theta J(\theta)\]
- \[\hat{\mathbf{m}} \leftarrow \frac{\mathbf{m}}{1-\beta_1^t}\]
- \[\hat{\mathbf{s}} \leftarrow \frac{\mathbf{s}}{1-\beta_2^t}\]
- \[\theta \leftarrow \theta+\eta\hat{m}\oslash\sqrt{\hat{\mathbf{s}}+\varepsilon}\]
- t는 (1부터 시작하는) 반복 횟수
- 단계 1,2,5는 모멘텀 최적화, RMSProp과 비슷
- 단계 3,4에서 \(\mathbf{m},\mathbf{s}\)는 0으로 초기화되기 때문에 훈련 초기에 0쪽으로 치우치게 된다. 그래서 이 두 단계가 훈련 초기에 \(\mathbf{m}, \mathbf{s}\)의 값을 증폭시키는 데 도움을 준다.
- 반복 초기에는 \(\mathbf{m}, \mathbf{s}\)를 증폭시켜주지만 반복이 많이 진행되면 단계 3,4의 분모는 1에 가까워져 거의 증폭되지 않는다.
- 모멘텀 감쇠 하이퍼파라미터 \(\beta_1\)은 보통 0.9로, 스케일 감쇠 하이퍼파라미터 \(\beta_2\)는 0.999로 초기화
optimizer = keras.optimizer.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
- Adam이 적응적 학습률 알고리즘이기 때문에 학습률 하이퍼파라미터 \(\eta\)를 튜닝할 필요가 적다.(기본값 0.001을 일반적으로 사용)
6. Adamax
- Adam은 시간에 따라 감쇠된 그래디언트의 \(l_2\) 노름으로 파라미터 업데이트의 스케일을 낮춘다.(\(l_2\) 노름은 제곱 합의 제곱근)
- Adamax는 \(l_2\) 노름을 \(l_\infty\) 노름으로 바꾼다
Adamax 알고리즘
- \[\mathbf{m} \leftarrow \beta_1\mathbf{m}-(1-\beta_1)\bigtriangledown_\theta J(\theta)\]
- \[\mathbf{s} \leftarrow max(\beta_2\mathbf{s}, \bigtriangledown_\theta J(\theta))\]
- \[\hat{\mathbf{m}} \leftarrow \frac{\mathbf{m}}{1-\beta_1^t}\]
- \[\theta \leftarrow \theta+\eta\hat{m}\oslash\sqrt{\mathbf{s}+\varepsilon}\]
- Adamax가 Adam보다 더 안정적
- 하지만 실제로 데이터셋에 따라 다르고 일반적으로 Adam의 성능이 더 낫다.
7. Nadam
- Adam 옵티마이저에 네스테로프 기법을 더한 것
- Adam보다 조금 더 빠르게 수렴
- 일반적으로 Nadam이 Adam보다 성능이 좋았지만 이따금 RMSProp이 나을 때도 있다.
모든 최적화 기법은 1차 편미분(야코비얀)에만 의존. 2차 편미분(헤시안)을 기반으로 한 뛰어난 알고리즘들이 있지만 하나의 출력마다 \(n\)개의 1차 편미분이 아니라 \(n^2\)개의 2차 편미분을 계산을해야 하기 때문에 메모리 용량을 넘어서거나 계산이 너무 느려서 심층 신경망에 적용하기 어렵다.
옵티마이저 비교(*=나쁨, *=보통, **=좋음)
| 클래스 | 수렴 속도 | 수렴 품질 |
|---|---|---|
| SGD | * | *** |
| Momentum | ** | *** |
| Nesterov | ** | *** |
| AdaGrad | *** | * (너무 일찍 멈춤) |
| RMSProp | *** | ** 또는 *** |
| Adam | *** | ** 또는 *** |
| Nadam | *** | ** 또는 *** |
| AdaMax | *** | ** 또는 *** |
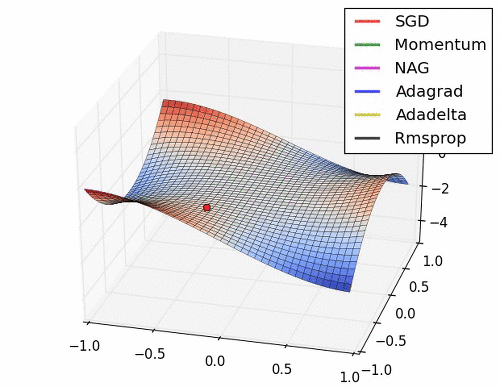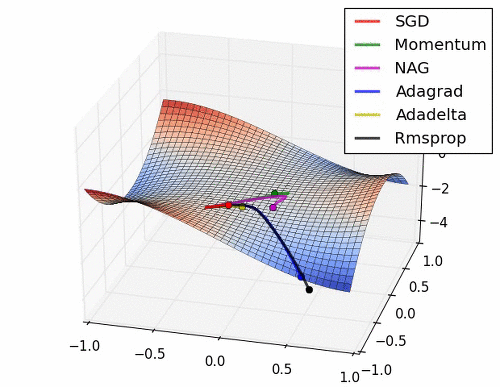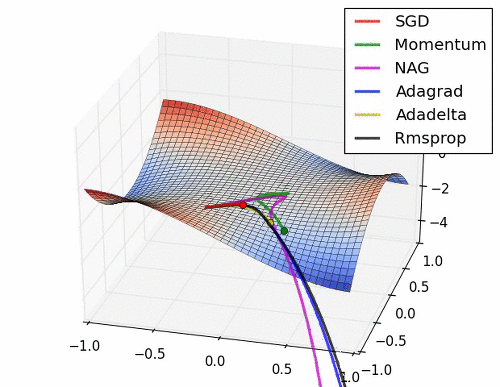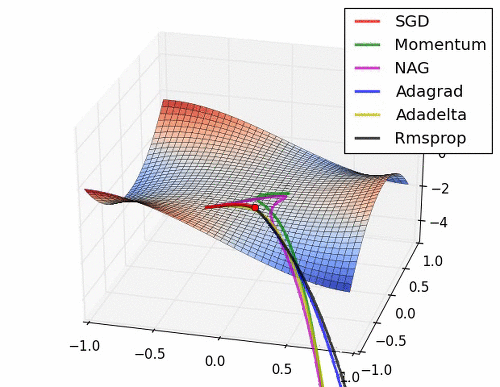
협곡에서 옵티마이저별 경로
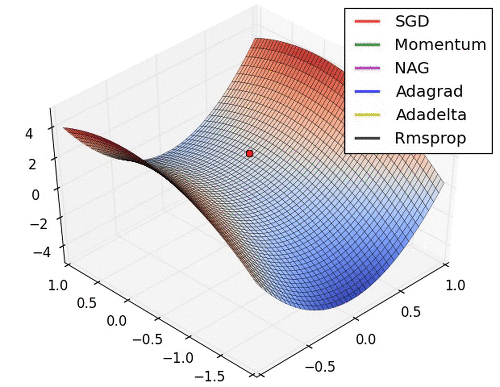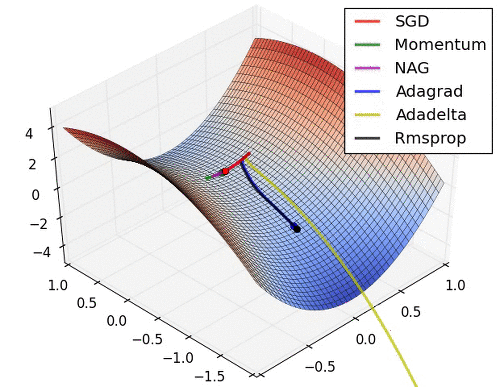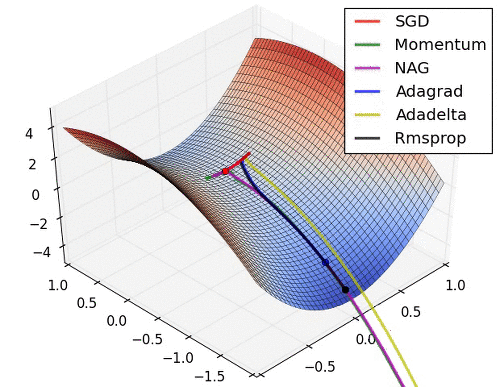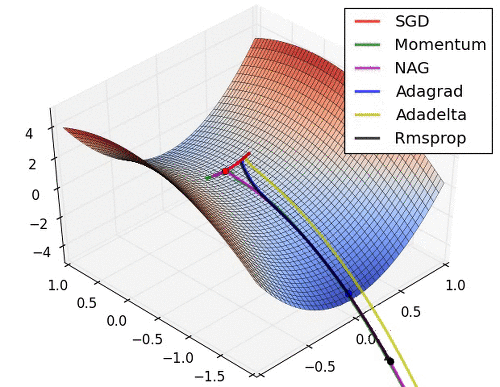
말안장점에서 옵티마이저별 경로