Published: Jul 10, 2020 by Dev-hwon
이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.
그래디언트 소실과 폭주 (Vanishing & Exploding Gradient)
- 그래디언트 소실(Vanishing Gradient): 알고리즘이 하위층으로 진행될수록 그래디언트가 점점 작아지는 경우
- 그래디언트 폭주(Exploding Gradient): 그래디언트가 점점 커져서 여러 층이 비정상적으로 큰 가중치를 갱신되어 알고리즘이 발산하는 경우
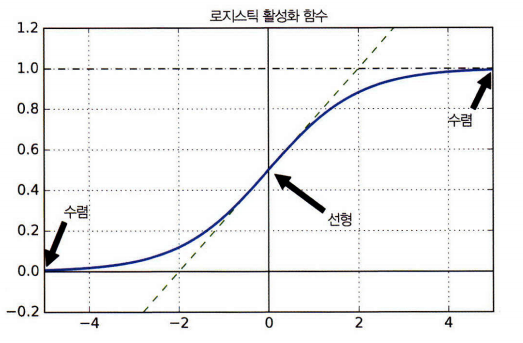
- 로지스틱 활성화 함수의 경우 입력이 커지면 0이나 1로 수렴해서 기울기가 0에 가까워짐
- 역전파가 될 때 사실상 신경망으로 전파할 그래디언트가 거의 없고 조금 있는 그래디언트는 최상위층에서부터 역전파가 진행되면서 점차 약해져서 실제로 아래쪽 층에는 아무것도 도달하지 않는다.
1. 글로럿과 He 초기화
- 글로럿과 벤지오가 불안정한 그래디언트 문제를 완화하는 방법 제안
- 각 층의 출력에 대한 분산이 입력에 대한 분산과 같아야 한다고 주장
- 역방향에서 층을 통과하기 전과 후의 그래디언트 분산이 동일
- \(fan_{avg}=(fan_{in}+fan_{out})\) 층의 입력 개수는 팬인 출력 개수는 팬아웃
글로럿 초기화
평균이 0이고 분산이 \(\sigma^2=\frac{1}{fan_{avg}}\)인 정규 분포
또는 \(r=\sqrt{\frac{3}{fan_{avg}}}\)일 때 -r과 +r사이의 균등 분포
르쿤 초기화
평균이 0이고 분산이 \(\sigma^2=\frac{1}{fan_{in}}\)인 정규 분포
또는 \(r=\sqrt{\frac{3}{fan_{in}}}\)일 때 -r과 +r사이의 균등 분포
- 글로럿 초기화를 하면 훈련 속도가 증가
| 초기화 전략 | 활성화 함수 | \(\sigma^2\)(정규분포) |
|---|---|---|
| 글로럿 | 활성화 함수 없음, tanh, logstic, softmax | \(1/fan_{avg}\) |
| He | ReLU 함수와 그 변종들 | \(2/fan_{in}\) |
| 르쿤 | SELU | \(1/fan_{in}\) |
- 케라스는 기본적으로 균등 분포의 글로럿 초기화를 사용
2. 수렴하지 않는 활성화 함수
- ReLU와 그 변종들, ELU, SELU는 저번 포스트에 자세히 다뤘습니다. 자세한 내용은 활성화 함수 포스트를 확인해주세요.
3. 배치 정규화 (Batch Normalization)
- 훈련하는 동안의 그래디언트 소실이나 폭주문제를 해결하기 위한 방법
- 세르게이 이오페, 치리슈티언 세게지가 제안
- 각 층에서 활성화 함수를 통과하기 전이나 후에 모델에 연산을 하나 추가
- 입력을 원점에 맞추고 정규화한 다음, 각 층에서 두 개의 새로운 파라미터로 결괏값의 스케일을 조정하고 이동
- 신경망의 첫 번째 층으로 배치 정규화를 추가하면 훈련세트를 표준화할 필요가 없다.
배치 정규화 알고리즘
- \[\mu_B=\frac{1}{m_B}\sum^{m_B}_{i=1}\mathbf{x}^{(i)}\]
- \[\sigma_B^2=\frac{1}{m_B}\sum^{m_B}_{i=1}(\mathbf{x}^{(i)}-\mu_B)^2\]
- \[\hat{\mathbf{x}}^{(i)}=\frac{\mathbf{x}^{(i)}-\mu_B}{\sqrt{\sigma_B^2+\varepsilon}}\]
- \[\mathbf{z}^{(i)}=\gamma\otimes\hat{\mathbf{x}}^{(i)}+\beta\]
\(\mu_B\)는 미니배치 B에 대해 평가한 입력의 평균 벡터(입력마다 하나의 평균)
\(\sigma_B\)도 미니배치에 대해 평가한 입력의 표준편차 벡터
\(m_B\)는 미니배치에 있는 샘플 수
\(\hat{\mathbf{x}}^{(i)}\)는 평균이 0이고 정규화된 샘플 i의 입력
\(\gamma\)는 층의 출력 스케일 파라미터 벡터(입력마다 하나의 스케일 파라미터가 존재)
\(\otimes\)는 원소별 곱셈(각 입력은 해당되는 출력 스케일 파라미터와 곱해진다.)
\(\beta\)는 층의 출력 이동(오프셋) 파라미터 벡더(입력마다 하나의 스케일 파라미터 존재). 각 입력은 해당 파라미터만큼 이동
\(\varepsilon\)은 분모가 0이 되는 것을 막기 위한 작은 숫자(전형적으로 \(10^{-5}\)). 안전을 위한 항(smoothing term) 이라고 함.
\(\mathbf{z}^{(i)}\)는 배치 정규화 연산의 출력. 즉 입력의 스케일을 조정하고 이동시킨 것
- 테스트 시에는 훈련이 끝난 후 전체 훈련 세트를 신경망에 통과시켜 배치 정규화 층의 각 입력에 대한 평균과 표준편차를 계산하여 예측할 때 배치 입력 평균과 표준 편차로 이 ‘최종’ 입력 평균과 표준편차를 대신 사용하는 방법이 있지만 대부분 층의 입력 평균과 표준편차의 이동 평균을 사용해 훈련하는 동안 최종 통계를 추정
- 케라스의 BatchNormalization 층은 이를 자동으로 수행
\(\gamma\)(출력 스케일 벡터)와 \(\beta\)(출력 이동 벡터)는 일반적인 역전파를 통해 학습
\(\mu\)(최종 입력 평균 벡터)와 \(\sigma\)(최종 입력 표준편차 벡터)는 지수 이동 평균을 사용하여 추정
\(\mu\)와 \(\sigma\)는 훈련하는 동안 추정되지만 훈련이 끝난 후에 사용
- 이미지넷 분류 작업에서 큰 성과
- 그래디언트 소실 문제가 크게 감소하여 tanh나 로지스틱 함수와 같은 수렴성을 가진 활성화 함수와도 사용 가능
- 가중치 초기화에 네트워크가 훨씬 덜 민감
- 규제와도 같은 역할을 하여 다른 규제 기법의 필요성 감소
- 단점: 모델의 복잡도가 커짐, 실행 시간 증가(대신 이전 층의 가중치를 바꾸어 이전 층과 배치 정규화 층이 합쳐진 결과를 내어 실행 시간을 단축시킬 수 있음)
4. 그래디언트 클리핑 (Gradient Clipping)
- 역전파될 때 일정 임곗값을 넘어서지 못하게 그래디언트를 자르는 방법
- 케라스에서 구현하려면 옵티마이저를 만들 때 clipvalue와 clipnorm 매개변수를 지정
optimizer = keras.optimizer.SGD(clipvalue=1.0)
model.complie(loss='mse', optimizer=optimizer)
위의 경우 그래디언트 벡터의 모든 원소를 -1.0과 1.0 사이로 클리핑.
그래디언트 벡터의 방향을 바꿀 수 있다.
- 그래디언트 클리핑이 그래디언트 벡터의 방향을 바꾸지 못하게 하려면 clipnorm을 지정하여 노름으로 클리핑



