Published: Jul 9, 2020 by Dev-hwon
활성화 함수 (Activation Function)
- 각 노드가 이전 노드들로부터 전달 받은 정보를 다음 노드에 얼마만큼 전달해 줄 것인가를 결정
- 선형 변환을 여러개 연결해도 얻을 수 있는 것은 선형 변환뿐
- 층 사이에 비선형성을 추가
- 비선형 활성화 함수가 있는 충분히 큰 심층 신경망은 이론적으로 어떤 연속 함수도 근사 가능
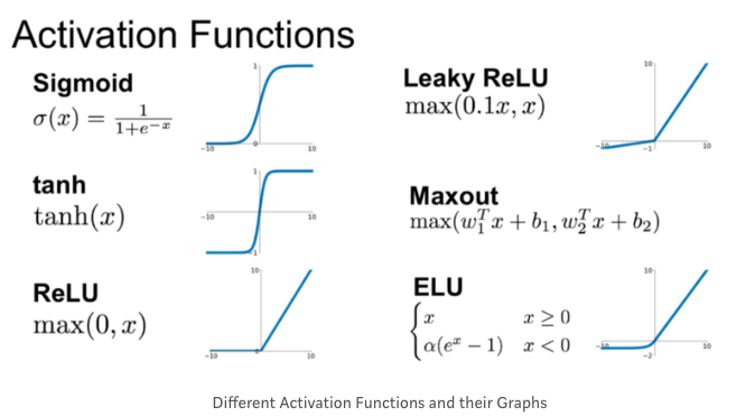
1. 시그모이드 함수 (Sigmoid function)
- Logistic 함수라고 불리기도 한다.
- 선형인 MLP에서 비선형 값을 얻기 위해 사용하기 시작
- 가장 일반적으로 사용되는 활성함수
- [0, 1]의 범위
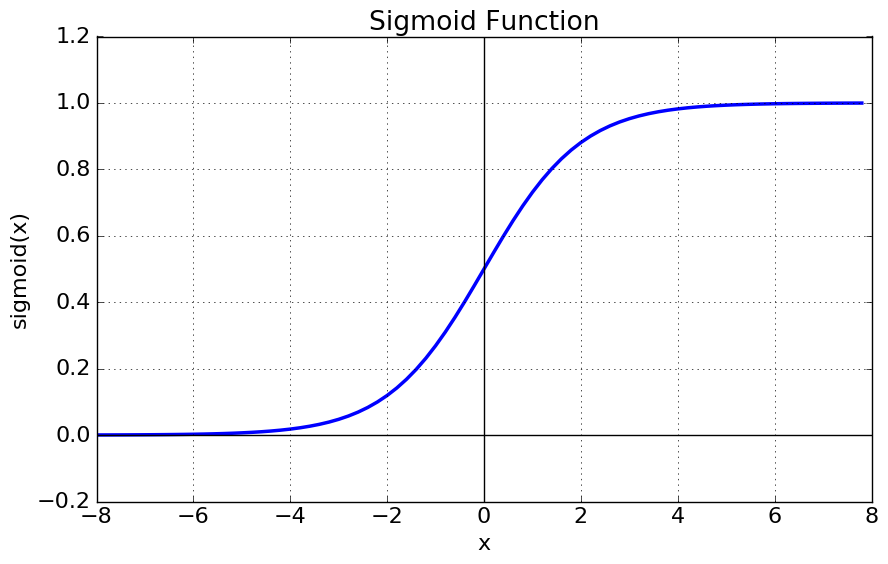
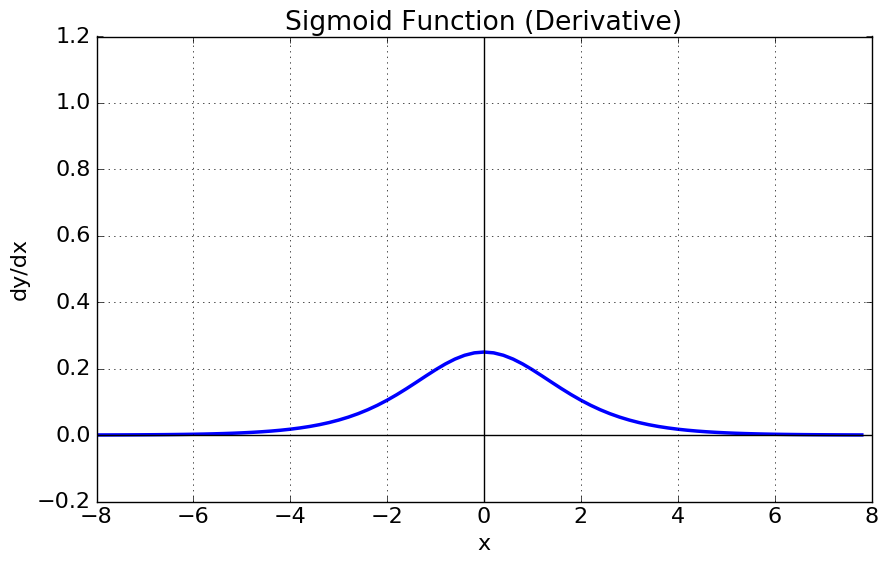
- 단점
1) gradient vanishing 현상이 발생한다. 미분함수에 대해 \(x=0\)에서 최댓값 \(\frac{1}{4}\)을 가지고, \(\begin{vmatrix} x \end{vmatrix}\)값이 커질 수록 미분값이 거의 0에 수렴
2) 함수값 중심이 0이 아니어서 학습이 느려질 수 있다. 만약 모든 x값들이 같은 부호(ex. for all x is positive) 라고 가정하면 파라미터 w에 대한 미분함수식은 \(\frac{\partial{L}}{\partial{w}}=\frac{\partial{L}}{\partial{a}}\frac{\partial{a}}{\partial{w}}\) 그리고 \(\frac{\partial{a}}{\partial{w}}=x\)이기 때문에, \(\frac{\partial{L}}{\partial{w}}=\frac{\partial{L}}{\partial{a}}x\) 이다. 위 식에서 모든 \(x\)가 양수라면 결국 \(\frac{\partial{L}}{\partial{w}}\)는 \(\frac{\partial{L}}{\partial{a}}\) 부호에 의해 결정된다. 따라서 한 노드에 대해 모든 파라미터w의 미분값은 모두 같은 부호를 같게된다. 따라서 같은 방향으로 update되는데 이러한 과정은 학습을 zigzag 형태로 만들어 느리게 만드는 원인이 된다.
3) exp 함수 사용시 비용이 크다.
2. \(tanh\) 함수 (Hyperbolic tangent function, 쌍곡 탄젠트 함수)
- 로지스틱 함수처럼 이 활성화 함수도 S자 모양, 연속적이며 미분 가능
- [-1, 1]의 범위, 훈련 초기에 각 층의 출력을 원점 근처로 모으는 경향, 이는 종종 빠르게 수렴되도록 도움
- 시그모이드 함수를 transformation 해서 얻을 수 있다.
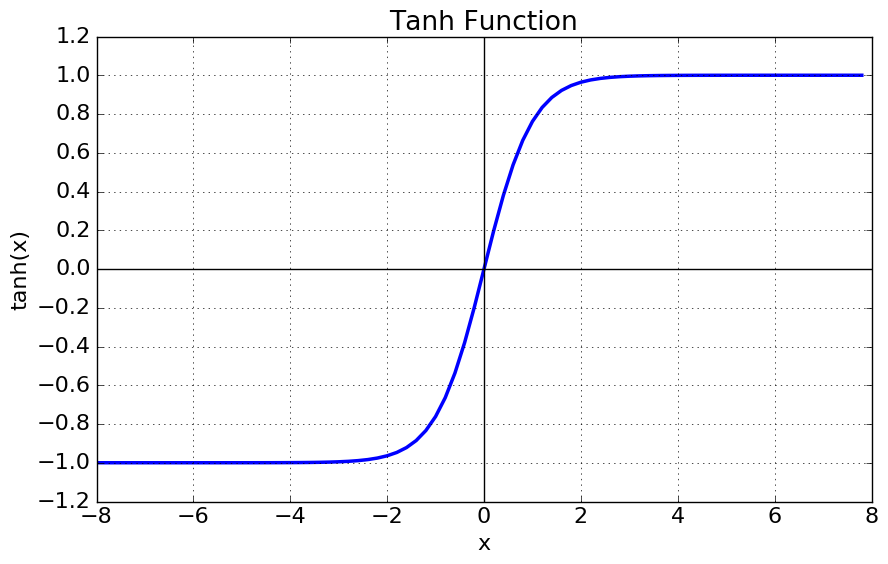
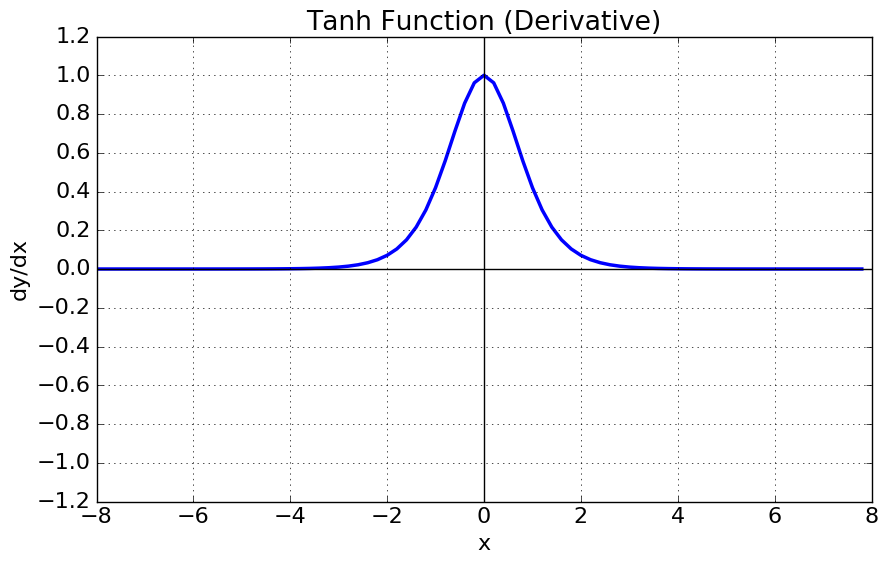
- 여전히 \(\begin{vmatrix} x \end{vmatrix}\)가 커지면 미분값이 소실되는 gradient vanishing 문제
3. ReLU 함수 (Rectified Linear Unit)
- 가장 많이 사용되는 활성화 함수(기본 활성화 함수)
- 연속적이지만 \(x=0\)에서 미분이 불가능(기울기가 갑자기 변해서 경사하강법이 엉뚱한 곳으로 튈 수 있다.)
- \(x<0\)일 경우 도함수는 0
- 잘 작동하고 계산 속도가 빠르다는 장점
- 출력에 최댓값이 없다는 점이 경사 하강법에 있는 일부 문제를 완화
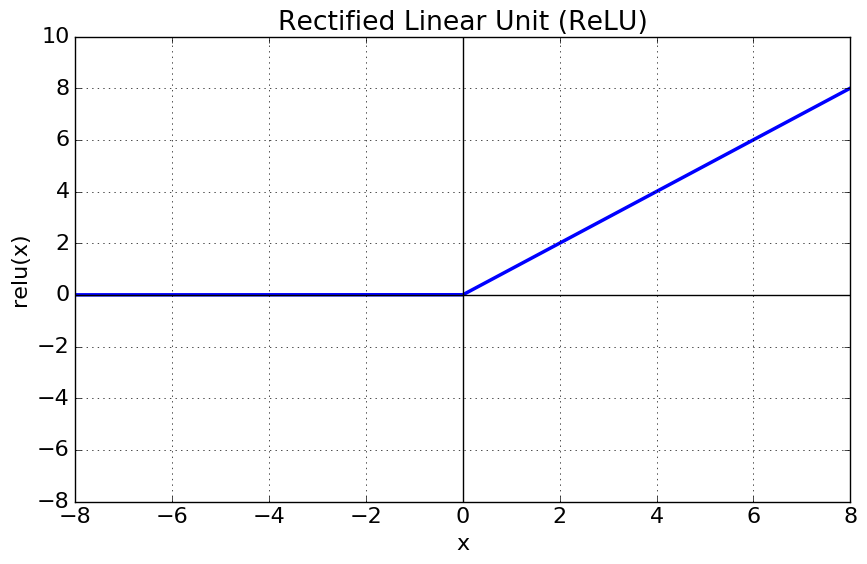
- \(x<0\)인 값들에 대해서 기울기가 0이기 때문에 0이외의 값을 출력하지 않는다는 의미에서 죽었다라고 하며 죽은 ReLU라고 한다.
- 훈련 세트에 있는 모든 샘플에 대해 입력의 가중치 합이 음수이면 ReLU 함수의 그래디언트가 0이 되므로 경사 하강법이 더는 작동하지 않는다.
4. LeakyReLU
- ReLU의 뉴런이 죽는 현상을 해결하기 위해 나온 함수
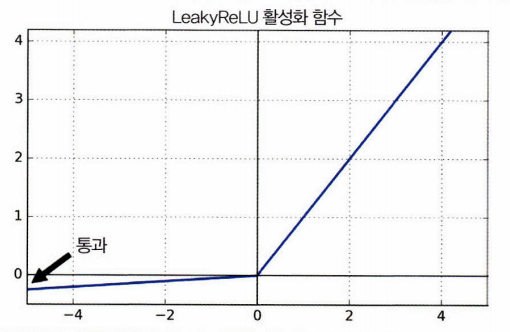
-
하이퍼파라미터 \(\alpha\)가 이 함수가 새는(leaky) 정도를 결정한다. 새는 정도란 \(x<0\)일 때 이 함수의 기울기이며, 일반적으로 0.01로 설정
- Bing Xu et al., “Empirical Evaluation of Rectified Activations in Convolutional Network” 논문에 따르면 LeakyReLU가 ReLU보다 항상 성능이 높은 것으로 나온다.
- \(\alpha=0.2\)로 하는 것이 0.01보다 더 나은 성능을 내는 것으로 보임.
5. RReLU (Randomized leaky ReLU)
- \(\alpha\)를 무작위로 선택하고 테스트 시에는 평균을 사용하는 방법
- 훈련 세트의 과대적함 위험을 줄이는 규제의 역할을 하는 것처럼 보임
6. PReLU (Parametric leaky ReLU)
- \(\alpha\)가 훈련하는 동안 학습되는 방법.(즉, 하이퍼파라미터가 아니고 다른 모델 파라미터와 마찬가지로 역전파에 의해 변경)
- 대규모 이미지 데이터셋에서는 ReLU보다 성능이 크게 앞섰지만, 소규모 데이터셋에서는 훈련 세트에 과대적합될 위험이 있다.
7. ELU (Exponential Linear Unit)
- 다른 모든 ReLU 변종의 성능을 앞지렀다.
- 훈련 시간이 줄고 신경망의 테스트 세트 성능도 더 높았다.
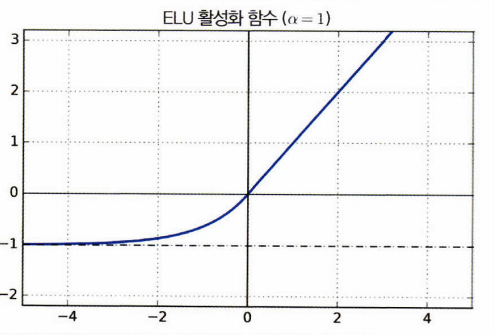
- \(x<0\)일 때 음숫값이 들어오므로 활성화 함수의 평균 출력이 0에 더 가깝다. 이는 그래디언트 소실 문제를 완화. 하이퍼파라미터 \(\alpha\)는 \(x\)가 큰 음숫값일 때 ELU가 수렴할 값을 정의
- \(x<0\)이어도 그래디언트가 0이 아니므로 죽은 뉴런을 만들지 않는다.
-
\(\alpha=1\)이면 이 함수는 \(x=0\)에서 급격히 변동하지 않으므로 \(x=0\)을 포함해 모든 구간에서 매끄러워 경사 하강법의 속도를 높여준다
- 단점: ReLU나 그 변종들보다 계산이 느리다.(훈련하는 동안에는 수렴 속도가 빨라서 느린 계산이 상쇄되지만 테스트 시에는 느릴 것)
8. SELU (Scaled ELU)
- ELU 활성화 함수의 변종
- 완전 연결 층만 쌓아서 신경망을 만들고 모든 은닉층이 SELU 활성화 함수를 사용하면 네트워크가 자기 정규화(self-normalized) 된다고 저자는 주장
- 훈련하는 동안 각 층의 출력이 평균 0과 표준편차 1을 유지하는 경향(그래디언트 소실과 폭주 문제를 막아준다.)
- 다른 활성화 함수보다 뛰어난 성능을 종종 보이지만 자기 정규화가 일어나기 위한 몇가지 조건이 존재
1) 입력 특성이 반드시 표준화(평균 0, 표준편차 1)되어야 한다.
2) 모든 은닉층의 가중치는 르쿤 정규분포 초기화로 초기화되어야 한다. 케라스에서는 kernel_initializer=’lecun_normal’로 설정
3) 네트워크는 일렬로 쌓은 층으로 구성되어야 한다. 순환 신경망이나 스킵 연결과 같은 순차적이지 않은 구조에서 사용하면 자기 정규화되는 것을 보장하지 않는다.
9. Maxout 함수
\[Maxout(x)=max(w_1^Tx+b_1,w_2^Tx+b_2)\]- ReLU가 가지는 모든 장점을 가졌으며, ReLU의 뉴런이 죽는 현상도 해결
- 계산량이 복잡하다는 단점
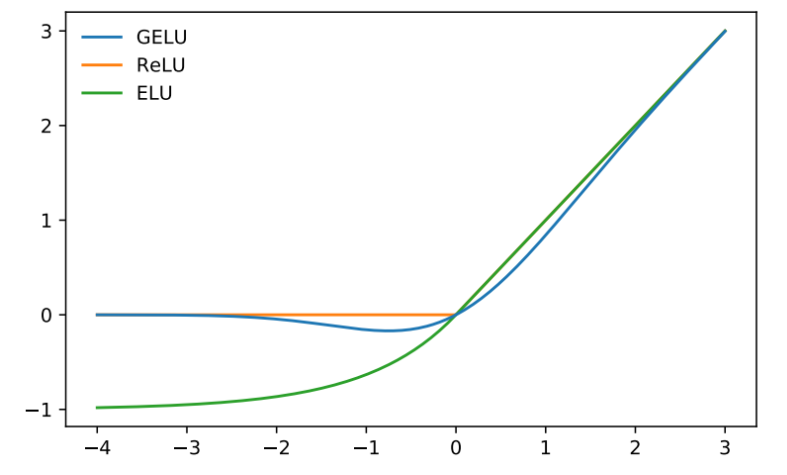
10. GELU (Gaussian Error Linear Unit)
- 2018년에 도입
- neuron output을 야기하는 switch
- 네트워크가 깊어질수록 잘 작동
- 비선형 함수
- adaptive dropout에 대한 수정된 기대로서, 뉴런의 출력이 더 높은 확률론적 관점을 제공
11. 활성화 함수 쓰는 방법
- 일반적으로 SELU > ELU > LeakyReLU(그리고 변종들) > ReLU > tanh > sigmoid 순
- 네트워크가 자기 정규화되지 못하는 구조라면 SELU 보단 ELU
- 실행 속도가 중요하다면 LeakyReLU(하이퍼파라미터를 더 추가하고 싶지 않다면 케라스에서 사용하는 기본값 \(\alpha\) 사용)
- 시간과 컴퓨팅 파워가 충분하다면 교차 검증을 사용해 여러 활성화 함수를 평가
- 신경망이 과대적합되었다면 RReLU
- 훈련세트가 아주 크다면 PReLU
- ReLU가 가장 널리 사용되는 활성화 함수이므로 많은 라이브러리와 하드웨어 가속기들이 ReLU에 특화되어 최적화. 따라서 속도가 중요하다면 ReLU가 가장 좋은 선택


