다층 퍼셉트론

Published: Jul 9, 2020 by Dev-hwon

이 내용은 핸즈온 머신러닝 2판 책을 보고 정리한 것 입니다.

다층 퍼셉트론 (Multi Layer Perceptron, MLP)

문제를 한꺼번에 풀지 말고 풀 수 있는 형태의 문제 여러개로 나누어 풀자
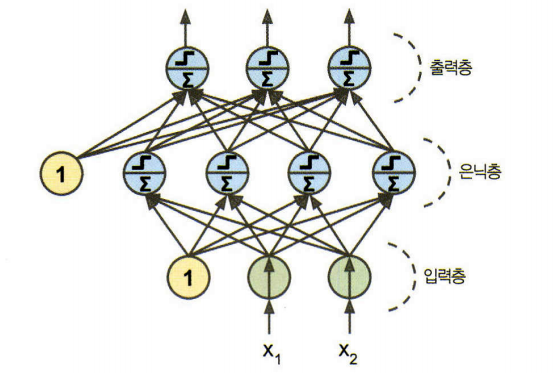
입력층 하나와 은닉층이라 불리는 하나 이상의 TLU층과 마지막 출력층으로 구성
입력층과 가까운 층을 보통 하위 층, 출력에 가까운 층을 상위 층

은닉층을 여러개 쌓아 올린 인공 신경망을 심층 신경망(deep neural network, DNN)이라고 한다.

1. 다층 퍼셉트론

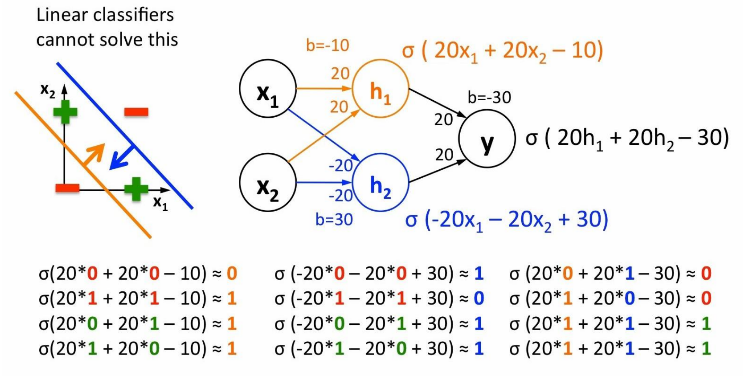
다층 퍼셉트론의 예측력이 우수한 이유

구분	로지스틱 회귀분석	의사결정나무	인공신경망
선의 수	1개	제한 없음	사용자 지정 (은닉층 및 노드의 수)
선의 방향	제약 없음	축에 수직	제약 없음

은닉노드의 역할

1) 은닉노드의 수가 인공신경망 복잡도(complexity)를 결정

2) 은닉노드가 많을수록 임의의 분류 경계면을 찾거나(분류 문제) 굴곡이 많은 함수를 추정(회귀 문제)할 수 있음

1.1 역전파 알고리즘

1) 각 훈련 새플에 대해 역전파 알고리즘이 먼저 예측을 만든다.(정방향 계산)

2) 역방향으로 각 층을 거치면서 각 연결이 오차에 기여한 정도를 측정(역방향 계산)

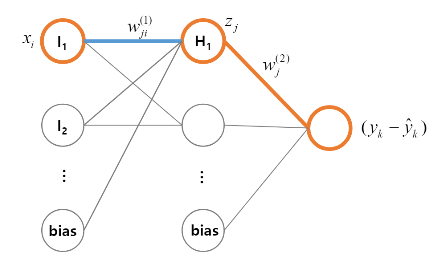
\(k\)번째 관측치의 오차

\[Err_k=\frac{1}{2}(y_k-\hat{y}_k)^2, \; \hat{y}_k=\sum^{p+1}_{j=1}w^{(2)}_jg(\sum^{d+1}_{i=1}w_{ji}^{(1)}x_i)\]

3) 오차가 감소하도록 가중치를 조정(경사 하강법)

\(j\)번째 은닉 노드와 출력 노드를 연결하는 가중치 \(w_j^{(2)}\)의 변화량

\[\frac{\partial Err_k}{\partial w_j^{(2)}}=\frac{\partial Err_k}{\partial \hat{y}_k}\cdot\frac{\partial \hat{y}_k}{\partial w_j^{(2)}}=(y_k-\hat{y}_k)\cdot z_j\]

\(j\)번째 은닉 노드와 \(i\)번째 입력 노드를 연결하는 가중치 \(w_{ji}^{(1)}\)의 변화량

\[\frac{\partial Err_k}{\partial w_{ji}^{(1)}}=\frac{\partial Err_k}{\partial \hat{y}_k}\cdot\frac{\partial \hat{y}_k}{\partial z_j}\cdot\frac{\partial z_j}{\partial h_j}\cdot\frac{\partial h_j}{\partial w_{ji}^{(1)}}=(y_k-\hat{y}_k)\cdot w_j^{(2)} \cdot z_j \cdot (1-z_j) \cdot x_i\]

2. 회귀를 위한 다층 퍼셉트론

출력 뉴런에 활성화 함수를 사용하지 않고 어떤 범위의 값도 출력되도록 한다.
항상 양수여야 한다면 출력층에 ReLU 활성화 함수를 사용할 수 있다.
또는 softplus 활성화 함수를 사용하여 z가 음수 일 때 0에 가까워지고 큰 양수 일수록 z에 가깝게 할 수 있다.
어떤 범위 한의 값을 예측하고 싶다면 로지스틱 함수나 하이퍼볼릭 탄젠트 함수를 사용하고 레이블의 스케일을 적절한 범위로 조정할 수 있다.
훈련에 사용하는 손실 함수는 전형적으로 평균 제곱 오차(MSE)
하지만 훈련 세트에 이상치가 많다면 평균 절댓값 오차(MAE)를 사용할 수 있다.(또는 둘을 조합한 후버(Huber)손실 사용)
회귀 MLP의 전형적인 구조

하이퍼파라미터	일반적인 값
입력 뉴런 수	특성마다 하나
은닉층 수	문제에 따라 다름, 일반적으로 1에서 5 사이
은닉층의 뉴런 수	문제에 따라 다름, 일반적으로 10에서 100사이
출력 뉴런 수	예측 차원마다 하나
은닉층의 활성화 함수	ReLU(또는 SELU)
출력층의 활성화 함수	없음, 또는 (출력이 양수일 때) ReLU/softplus 나 (출력을 특정 범위로 제한할 때) logistic/tanh 사용
손실 함수	MSE나 (이상치가 있다면) MAE/Huber

3. 분류를 위한 다층 퍼셉트론

이진 분류

로지스틱 활성화 함수를 가진 출력 뉴런 하나 필요. 출력은 0과 1사이의 실수로 이를 양성 클래스에 대한 예측 확률로 해석.

다중 레이블 이진 분류

로지스틱 활성화 함수를 가진 출력 뉴런 여러개로 다중 레이블 분류가 가능. 각 샘플이 3개 이상의 클래스 중 한 클래스만 속하여야 한다면 출력층에 소프트 맥스 활성화 함수를 사용. 모든 예측 확률을 0과 1사이로 만들고 더했을 때 1이 되도록 한다. 이를 다중 분류라고 함. 손실 함수로는 일반적으로 크로스 엔트로피 손실(또는 로그 손실)을 선택

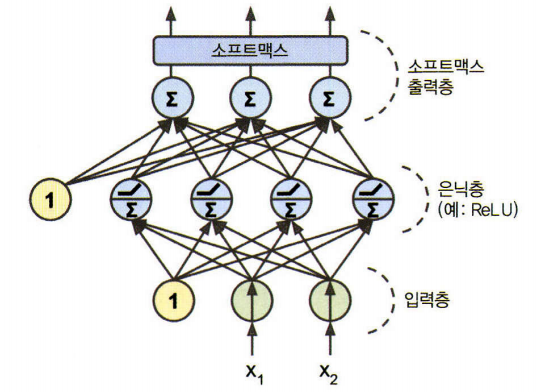
분류 MLP의 전형적인 구조

하이퍼파라미터	이진 분류	다중 레이블 분류	다중 분류
입력층과 은닉층	회귀와 동일	회귀와 동일	회귀와 동일
출력 뉴런 수	1개	레이블마다 1개	클래스마다 1개
출력층의 활성화 함수	로지스틱 함수	로지스틱 함수	소프트맥스 함수
손실 함수	크로스 엔트로피	크로스 엔트로피	크로스 엔트로피