Published: Jan 15, 2020 by Dev-hwon

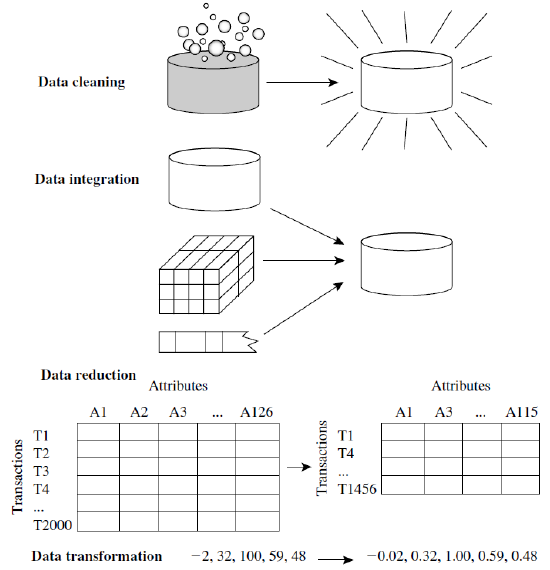
Data Preprocessing

• 실제 데이터베이스는 일반적으로 대용량이며, 여러개의 이질적인 데이터 원천에서 취합되기 때문에 노이즈에 취약, 일관성이 떨어짐

Major Tasks in Preprocessing

• Data Cleaning
  • Handling missing data (결측치 채우기)
  • Smoothing noisy data (노이즈 데이터 조정)
• Data Integration
  • Identifying duplicated data (중복된 데이터 식별)
• Data Reduction
  • Removing unrelated data (관련 없는 데이터 삭제)
• Data Transformation
  • Transforming data for better analysis (보다 나은 분석을 위해 데이터 변환)

Handling missing values (결측치)

1. 행(튜플) 무시하기 - 분류 분석시 클래스 라벨이 없는 경우 일반적으로 사용, 효과적인 방법X
2. 수작업으로 결측치 채우기 - 많은 시간 소요, 결측치가 많은 대량의 데이터에는 부적합
3. 글로벌 상수값을 이용하여 결측치 채우기 - “Unknown” 같은 라벨로 대체, 마이닝 프로그램이 유의미한 개념으로 이 값을 고려할 수 있음
4. 해당 속성의 중심경향 측정값 사용(평균, 중위수) - 대칭인 경우 평균, 편향된 경우 중위수 사용
5. 주어진 튜플과 동일한 클래스에 속하는 모든 샘플의 속성 평균이나 중위수 이용
6. 가장 가능성 높은 값으로 결측치 채우기 - 회귀분석이나 베이지안, 의사결정트리 등 이용

• 3~6은 데이터 왜곡, 대체값이 정확하지 않을 수 있음
• 6을 많이 사용, 다른 방법과 비교해볼 때 현 데이터를 사용하여 결측치 예측

Noisy Data

• 노이즈는 측정 변수의 랜덤 오류나 분산에 해당함

1. Binning(비닝)
   • 근접한 다른 값을 참고하여 정렬한 데이터 값을 평활화
   • 정렬한 값을 빈의 수인 버킷 수 만큼 나눔

ex) 4,8,15,21,21,24,25,28,34

1) 동일 빈도 빈으로 분할

Bin 1: 4,8,15
Bin 2: 21,21,24
Bin 3: 25,28,34

2) 빈 평균으로 평활화

Bin 1: 9,9,9
Bin 2: 22,22,22
Bin 3: 29,29,29

3) 빈 경계로 평활화

Bin 1: 4,4,15
Bin 2: 21,21,24
Bin 3: 25,25,34

1. Others
   • Regression(회귀분석) - 따로 포스트 올릴 예정
   • Outlier analysis(이상치 분석) - 클러스터링(군집화)로 찾아냄, 직관적으로 군집 외부에 존재하는 값

Data integration

1. Entity identification problem(개체 식별 문제)
   • 다양한 데이터 원천에서 수집한 데이터를 결합하여 통합하는 작업을 포함
2. Redundancy and Correlation analysis(중복과 상관관계 분석)
   • 다른 속성으로 계산 가능한 경우, 속성이나 차원의 비일치는 결과 데이터 집합의 중복을 발생
   • 몇가지 중복은 상관분석으로 확인 가능
   • Nominal data - \(\chi^2\) test
   • Numeric attributes - 상관계수, 공분산

2-1. \(\chi^2\) Correlation Test for Nominal Data

• 귀무가설: A와 B는 독립이다.

• 예측 빈도수: \(e_{ij} = { {o_{i.}o_{.j} } \over e_{ij} }\)
• \(\chi^2((c-1)(r-1)) = \sum^c_{i=1}\sum^r_{j=1} { (o_{ij}-e{ij})^2 \over e_{ij} }\), degree of freedom: (c-1)(r-1)

2-2. Correlation Coefficent for Numeric Data

• 두 속성 A와 B의 상관관계는 상관계수로 계산할 수 있다.

  \[\gamma_{A,B} = { {\sum^n_{i=1}(a_i-\bar A)(b_i-\bar B) \over n\sigma_A \sigma_B} } = { {\sum^n_{i=1}(a_ib_i)-n \bar A \bar B} \over n\sigma_A\sigma_B }\]

• > 0 : 양의 상관 관계, = 0 : 독립, < 0 : 음의 상관 관계

2-3. Covariance of Numeric Data

• 2개의 속성이 어느 정도 같은 방향으로 변동하는지를 정량적으로 평가한 값

\(Cov(A,B) = E(A\cdot B)-\bar A \bar B\) \(r_{A,B} = { {Cov(A,B)} \over \sigma_A \sigma_B }\)

Data reduction

• 대용량 데이터에 대한 복잡한 데이터 분석과 마이닝은 실행하기 어렵거나 불가능한 경우가 많음
• 작은 양의 데이터 표현 결과를 얻게 되더라도 원데이터의 완결성을 유지하기 위해 좀 더 효과적이고 원래 데이터와 거의 동일한 분석 결과
• 차원 축소: wavelet, 주성분 분석(PCA)
• 숫자 축소: 회귀, 히스토그램, 클러스터링, 샘플링

1) wavelet

2) Principal Component Analysis (PCA)

• K <= n을 만족하는 데이터를 표현하는데 가장 잘 사용할 수 있는 K개의 n차원 직교 벡터를 찾는 방법
• 원데이터는 좀 더 작은 공간에 투영되게 차원이 축소됨
• 이전에 고려하지 않은 관계를 도출하며 해석도 기존에 몰랐던 새로운 결과가 될 수 있음
• 절차
  1. Normalized(정규화)
  2. k개의 직교 벡터 계산
  3. 주성분은 내림차순의 중요도나 힘을 갖고 있다. 데이터에 대한 새로운 축의 집합으로 기능
  4. 낮은 변동을 갖는 약한 성분 제거하여 데이터 크기 축소

3) Feature Selection

• 분석용 데이터 집합은 수백개의 속성을 갖고 있으며 해당 속성은 마이닝 작업에 무관하거나 중복된 속성일 수 있음
• 무관한 속성이나 중복된 속성을 제거하여 데이터 집합 축소
• 속성의 개수를 줄이고 해당 패턴을 이해하기 쉽도록 해줌
• 방법

4) Regression

• 회귀는 주어진 데이터를 근사하는데 사용
• 자세한 내용은 나중에 따로 포스트 작성 예정

5) Histogram

• 비닝을 사용하여 데이터 분포를 근사화

6) Clustering

• 개체를 그룹 또는 클러스터로 분할
• 자세한 내용은 나중에 따로 포스트 작성 예정

7) Sampling

• 대표적인 하위 집합을 선택, 데이터 축소

Data Transformation and Discretization(데이터 변환과 구분)

• 마이닝 프로세스를 효율적으로 수행하고, 발견된 패턴을 쉽게 이해 할 수 있도록 해줌 1.Smoothing 2.Attribute construction(속성 또는 특성 구축) 3.Aggregation 4.Normalization(정규화) 5.Discretization 6.명목 데이터에 대한 개념계층 생성

1. Normalization
   • 측정단위는 데이터 분석에 영향을 줄 수 있음
   • 모든 속성에 동일한 가중치 적용
   • 방법 1) 최소-최대 정규화
   \[{v_i}' = { {v_i - min_A} \over max_A-min_A}(new\_max_A-new\_min_A)+new\_min_A\]

2) Z-score 정규화 - 평균과 표준편차를 정규화(최소-최대값을 모를 경우, 이상치에의해 최소-최대 정규화가 영향을 받을 때)

3) 십진 스케일링에 의한 정규화

• 10의 배수 값으로 이동시켜 정규화