Published: Jan 14, 2020 by Dev-hwon

Data similarity(데이터 유사도)

데이터 유사도란 두 데이터가 얼마나 같은지 나타내주는 척도이다.

Basic data structure

1. data matrix (n object X p attributes)

$$\begin{bmatrix} x_{11} & \cdots & x_{1f} & \cdots & x_{1p}\\ \cdots & \cdots & \cdots & \cdots & \cdots\\ x_{i1} & \cdots & x_{if} & \cdots & x_{ip}\\ \cdots & \cdots & \cdots & \cdots & \cdots\\ x_{n1} & \cdots & x_{nf} & \cdots & x_{np} \end{bmatrix}$$

1. similarity matrix (n objects X n objects)

$$\begin{bmatrix} 0 & & & & \\ sim(2,1) & 0 & & & \\ sim(3,1) & sim(3,2) & 0 & & \\ \vdots & \vdots & \vdots & & \\ sim(n,1) & sim(n,2) & \cdots & \cdots & 0 \end{bmatrix}$$

1. disimilarity matrix (n objects X n objects)

• sim(i,j) = 1 - d(i,j)

$$\begin{bmatrix} 0 & & & & \\ d(2,1) & 0 & & & \\ d(3,1) & d(3,2) & 0 & & \\ \vdots & \vdots & \vdots & & \\ d(n,1) & d(n,2) & \cdots & \cdots & 0 \end{bmatrix}$$

---

Similarity and Distance Measures

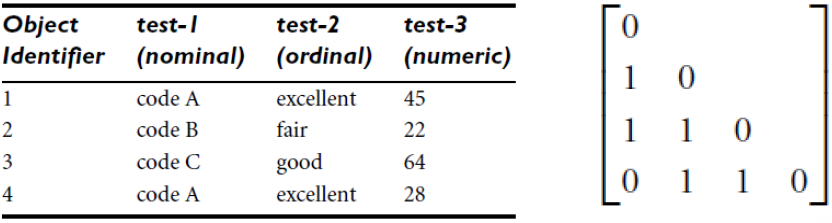
1. For nominal attributes

• $$d(i,j) = { {p-m} \over p }$$
• m = number of matches
• p = total number of attributes descibing the objects

ex)

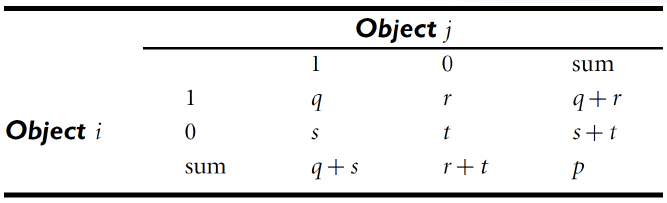
2. For binary attributes

• For symmetric binary attributes (0과 1 모두 중요)

$$d(i,j) = { {r+s} \over {q+r+s+t}}$$

• For asymmetric binary attributes (1이 더 중요)

$d(i,j) = { {r+s} \over {q+r+s}}$ (Jaccard Coefficent라고도 불림)

(ex)

3. For numeric attributes

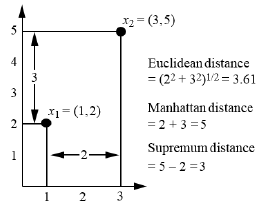
1) Euclidean Distance

$$d(i,j) = \sqrt{\sum^p_{k=1}(x_{ik}-x_{jk})^2}$$

2) Manhattan Distance

$$d_{manhattan}(i,j) = \sum^p_{k=1}\left | x_{ik}-x_{jk} \right |$$

• Euclidean, Manhattan Distance가 만족해야하는 조건
  • 음이 아닌 수
  • Identify of indiscernibles
  • 대칭
  • Triangle inequality

3) Minkowski Distance

$$d(i,j) = (\sum^p_{k=1} \left | x_{ik}-x_{jk} \right |^r)^{1/r}$$

• r=1 : Manhattan (L1 norm)
• r=2 : Euclidean (L2 norm)
• r= $\infty$ : Supremum (Lmax norm, L$\infty$ norm)

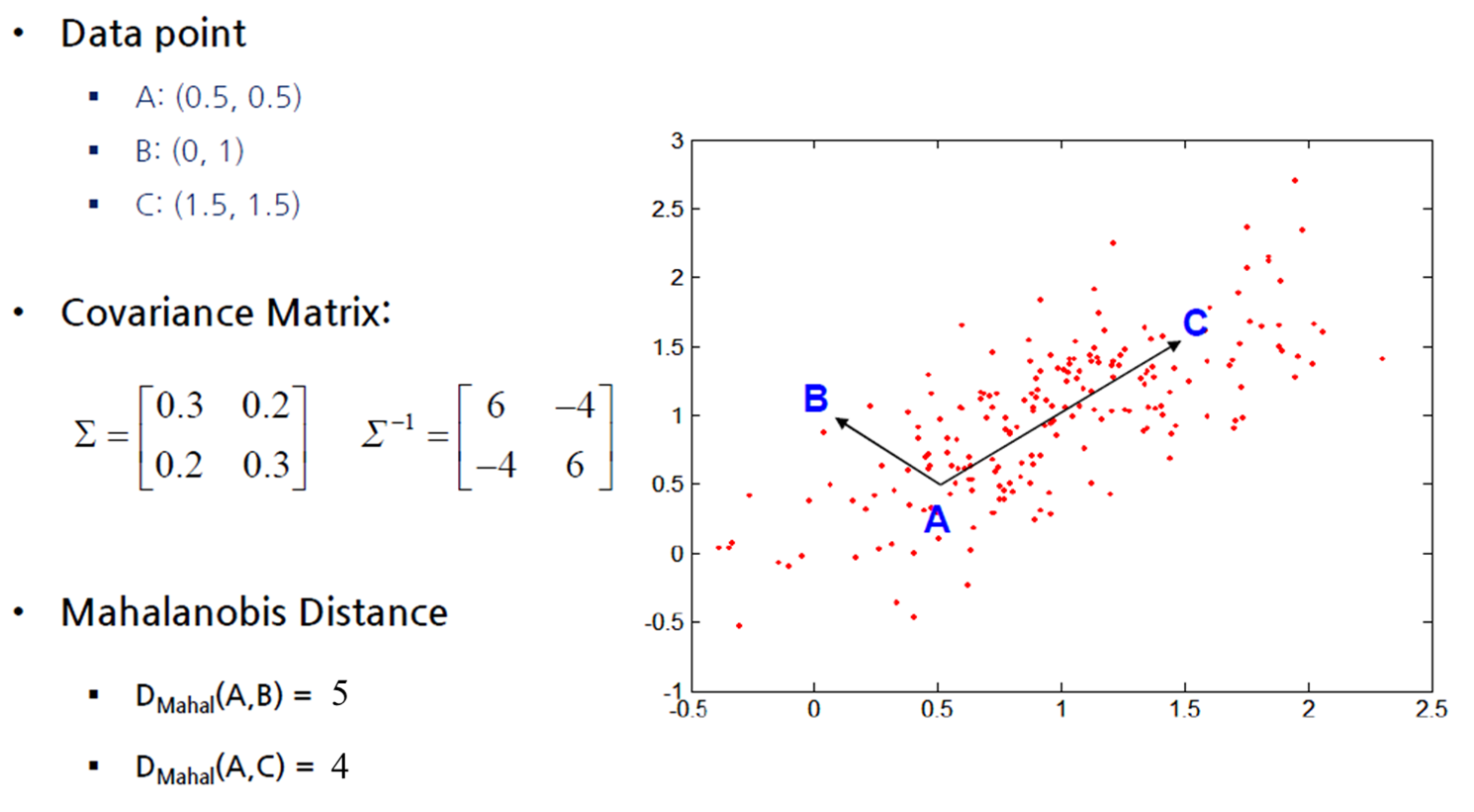
4) Mahalanobis Distance

• 데이터 분포를 고려하기 위해 사용

$$Mahalanobis(X,Y) = (X-Y)^T{\sum}^{-1}(X-Y)$$

4. For ordinal attributes

• ordinal attributes는 순서 or 순위가 있지만 크기는 알 수 없다.
  • 1) 등급에 따라 점수를 준다.
  • 2) normalizes
  • 3) Euclidean Distance 이용
    

5. For mixed attributes

1) 각 속성 유형을 그룹화하고 각 유형에 대해 개별적으로 군집화와 같은 데이터 마이닝 수행하는 방법

2) 모든 속성 유형을 함께 처리하여 한 개의 분석을 실행하는 방법 -> 여러 속성을 단 한개의 차이 행렬로 연결하고 모든 의미 있는 속성을 공통된 범위 척도 [0.0, 1.0]으로 만드는 방법

$$d(i,j) = { {\sum^p_{f=1}\delta_{ij}^{(f)}d_{ij}^{(f)} \over \sum^p_{f=1}\delta_{ij}^{(f)}} }$$

$\delta_{ij}^{(f)}=0$일 때,

1) $x_{if}$나$x_{jf}$가 없는 경우 2) $x_{if}=x_{jf}=0$이고 속성 f가 비대칭 이진값 $d_{ij}^{(f)}$인 경우

• if f is numeric:

$d_{ij}^{(f)} = { {\left | x_{if} - x_{jf} \right |} \over max_h x_{hf} - min_h x_{hf} }$

• if f is nominal, binary or ordinal: 따로 구하는 방법과 같음

---

cosine similarity(코사인 유사도)

• 내적공간의 두 벡터의 유사도를 측정함
• 두 벡터간 각도의 코사인으로 측정하며 두 벡터가 동일한 방향을 향하고 있는지 여부를 판단
• 종종 텍스트 분석에서 문서의 유사도를 측정하는데 사용

Term-Frequency 벡터

• 일반적으로 매우 길고 데이터 값은 별로 없음, 따라서 대부분 0의 값을 가짐
• 일반적으로 거리 측정값은 희소한 숫자형 데이터에 대해서는 적합하지 않음
• 따라서 2개의 문서가 공통으로 보유하고 있는 단어와 해당 단어의 발생 빈도에 초점

$sim(x,y) = {x\cdot y \over \left \| x \right \| \left \| y \right \|}$, $\left \| x \right \|$는 벡터 x에 대한 유클리드 노름, difined as $\sqrt{x_1^2+x_2^2+\cdots}$

ex)

속성이 이진값일 때

• 코사인 유사도는 공유된 특성이나 속성으로 해석
• $$sim(x,y) = { {x\cdot y} \over {x\cdot x + y\cdot y - x\cdot y} }$$
• x 또는 y가 소유한 속성의 수에 대해 x와 y가 고유한 속성의 개수 비율
• 타니모토계수나 타니모토 거리라고 함